
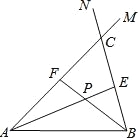
【题目】在线段AB的同侧作射线AM和BN,若∠MAB与∠NBA的平分线分别交射线BN,AM于点E,F,AE和BF交于点P.如图,点点同学发现当射线AM,BN交于点C;且∠ACB=60°时,有以下两个结论:
①∠APB=120°;②AF+BE=AB.
那么,当AM∥BN时:
(1)点点发现的结论还成立吗?若成立,请给予证明;若不成立,请求出∠APB的度数,写出AF,BE,AB长度之间的等量关系,并给予证明;
(2)设点Q为线段AE上一点,QB=5,若AF+BE=16,四边形ABEF的面积为32![]() ,求AQ的长.
,求AQ的长.
【答案】(1)、∠APB=90°,AF+BE=2AB;理由见解析;(2)、AQ=4![]() ﹣3或4
﹣3或4![]() +3
+3
【解析】
试题分析:(1)、由角平分线和平行线整体求出∠MAB+∠NBA,从而得到∠APB=90°,最后用等边对等角,即可;(2)、先根据条件求出AF,FG,求出∠FAG=60°,最后分两种情况讨论计算.
试题解析:(1)、原命题不成立,新结论为:∠APB=90°,AF+BE=2AB(或AF=BE=AB),
理由:∵AM∥BN, ∴∠MAB+∠NBA=180°, ∵AE,BF分别平分∠MAB,NBA,
∴∠EAB=![]() ∠MAB,∠FBA=
∠MAB,∠FBA=![]() ∠NBA, ∴∠EAB+∠FBA=
∠NBA, ∴∠EAB+∠FBA=![]() (∠MAB+∠NBA)=90°, ∴∠APB=90°,
(∠MAB+∠NBA)=90°, ∴∠APB=90°,
∵AE平分∠MAB, ∴∠MAE=∠BAE, ∵AM∥BN, ∴∠MAE=∠BAE, ∴∠BAE=∠BEA, ∴AB=BE,
同理:AF=AB, ∴AF=+BE=2AB(或AF=BE=AB);
(2)、如图1,
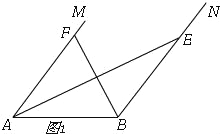
过点F作FG⊥AB于G, ∵AF=BE,AF∥BE, ∴四边形ABEF是平行四边形, ∵AF+BE=16,
∴AB=AF=BE=8, ∵32![]() =8×FG, ∴FG=4
=8×FG, ∴FG=4![]() , 在Rt△FAG中,AF=8, ∴∠FAG=60°,
, 在Rt△FAG中,AF=8, ∴∠FAG=60°,
当点G在线段AB上时,∠FAB=60°,
当点G在线段BA延长线时,∠FAB=120°,
①如图2,

当∠FAB=60°时,∠PAB=30°, ∴PB=4,PA=4![]() , ∵BQ=5,∠BPA=90°, ∴PQ=3,
, ∵BQ=5,∠BPA=90°, ∴PQ=3,
∴AQ=4![]() ﹣3或AQ=4
﹣3或AQ=4![]() +3.
+3.
②如图3,
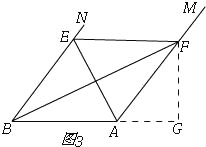
当∠FAB=120°时,∠PAB=60°,∠FBG=30°, ∴PB=4![]() , ∵PB=4
, ∵PB=4![]() >5,
>5,
∴线段AE上不存在符合条件的点Q,
∴当∠FAB=60°时,AQ=4![]() ﹣3或4
﹣3或4![]() +3.
+3.


科目:初中数学 来源: 题型:
【题目】如图,在矩形 ABCD中, AB16 , BC18 ,点 E在边 AB 上,点 F 是边 BC 上不与点 B、C 重合的一个动点,把△EBF沿 EF 折叠,点B落在点 B' 处.
(I)若 AE0 时,且点 B' 恰好落在 AD 边上,请直接写出 DB' 的长;
(II)若 AE3 时, 且△CDB' 是以 DB' 为腰的等腰三角形,试求 DB' 的长;
(III)若AE8时,且点 B' 落在矩形内部(不含边长),试直接写出 DB' 的取值范围.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1+∠2=180°,∠B=∠D.说明AB∥CD的理由.
补全下面的说理过程,并在括号内填上适当的理由
解:∵∠1+∠2=180°(已知)
∠2=∠AHB( )
∴ (等量代换)
∴DE∥BF( )
∴∠D=∠ ( )
∵∠ =∠B(等量代换)
∴AB∥CD( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直角△ABC的三个顶点分别是A(﹣3,1),B(0,3),C(0,1)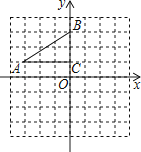
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1;
(2)分别连结AB1、BA1后,求四边形AB1A1B的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育课上,20人一组进行足球比赛,每人射点球5次,已知某一组的进球总数为49个,进球情况记录如下表,其中进2个球的有x人,进3个球的有y人,若(x, y)恰好是两条直线的交点坐标,则这两条直线的解析式是( )

A. y=x+9与![]() B. y=-x+9与
B. y=-x+9与![]()
C. y=-x+9与![]() D. y=x+9与
D. y=x+9与![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量出楼房AC的高度,从距离楼底C处60 ![]() 米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:
米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1: ![]() 的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈
的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈ ![]() ,计算结果用根号表示,不取近似值).
,计算结果用根号表示,不取近似值).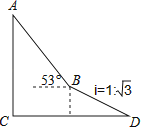
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《算法统宗》是中国古代数学名著,作者是我国明代数学家程大位.在《算法统宗》中记载:“以绳测井,若将绳三折测之,绳多4尺,若将绳四折测之,绳多1尺,绳长井深各几何?”
译文:“用绳子测水井深度,如果将绳子折成三等份,井外余绳4尺;如果将绳子折成四等份,井外余绳1尺.问绳长、井深各是多少尺?”
设井深为x尺,根据题意列方程,正确的是( )

A. 3(x+4)=4(x+1) B. 3x+4=4x+1
C. 3(x﹣4)=4(x﹣1) D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com