
【题目】已知∠AOB=120°,∠COD=60°,OE平分∠BOC
(1)如图①.当∠COD在∠AOB的内部时
①若∠AOC=39°40′,求∠DOE的度数;
②若∠AOC=α,求∠DOE的度数(用含α的代数式表示),
(2)如图②,当∠COD在∠AOB的外部时,
①请直接写出∠AOC与∠DOE的度数之间的关系;
②在∠AOC内部有一条射线OF,满足∠AOC+2∠BOE=4∠AOF,写出∠AOF与∠DOE的度数之间的关系.
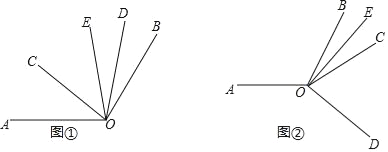
【答案】(1)①19°50′;②∠DOE=![]() ;(2)①∠AOC=2∠DOE;②∠DOE=∠AOF+30°.
;(2)①∠AOC=2∠DOE;②∠DOE=∠AOF+30°.
【解析】
(1)①②根据角平分线的定义和角的和差即可得到结论;
②根据角平分线的定义和角的和差即可得到结论;
(2)①根据已知条件得到∠AOC=120°+∠BOC,∠DOE=60°+∠COE,根据角平分线的定义得到∠COE=![]() ∠BOC,等量代换即可得到结论;
∠BOC,等量代换即可得到结论;
②如图,由①知,∠AOC=2∠DOE,根据∠AOC+2∠BOE=4∠AOF,化简即可得到结论.
(1)①∵∠AOB=120°,∠COD=60°,∠AOC=39°40′,
∴∠BOC=∠AOB﹣∠AOC=120°﹣39°40′=80°20′,
∵OE平分∠BOC,
∴∠COE=![]() ∠BOC=40°10′,
∠BOC=40°10′,
∴∠DOE=∠COD﹣∠COE=19°50′;
②∵∠AOB=120°,∠COD=60°,∠AOC=α,
∴∠BOC=∠AOB﹣∠AOC=120°﹣α,
∵OE平分∠BOC,
∴∠COE=![]() ∠BOC=60°﹣
∠BOC=60°﹣![]() α,
α,
∴∠DOE=![]() ;
;
(2)①∵∠AOC=120°+∠BOC,∠DOE=60°+∠COE,
∵OE平分∠BOC,
∴∠COE=![]() BOC,
BOC,
∴∠AOC=2∠DOE;
②如图,
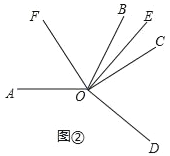
由①知,∠AOC=2∠DOE,
∵∠AOC+2∠BOE=4∠AOF,
∴∠AOC+∠BOC=∠AOC+∠AOC﹣120°=2∠AOC﹣120°=4∠DOE﹣120°=4∠AOF,
∴∠DOE=∠AOF+30°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( ) 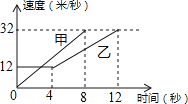
A.乙前4秒行驶的路程为48米
B.在0到8秒内甲的速度每秒增加4米/秒
C.两车到第3秒时行驶的路程相等
D.在4至8秒内甲的速度都大于乙的速度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的对角线交于点O,AB∥CD,O是BD的中点.
(1)求证:△ABO≌△CDO;
(2)若BC=AC=4,BD=6,求△BOC的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1+∠2=180°,∠B=∠D.说明AB∥CD的理由.
补全下面的说理过程,并在括号内填上适当的理由
解:∵∠1+∠2=180°(已知)
∠2=∠AHB( )
∴ (等量代换)
∴DE∥BF( )
∴∠D=∠ ( )
∵∠ =∠B(等量代换)
∴AB∥CD( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个正整数可以表示为两个连续奇数的平方差,那么称该正整数为“和谐数”如(8=32﹣12,16=52﹣32,即8,16均为“和谐数”),在不超过2017的正整数中,所有的“和谐数”之和为( )
A. 255054 B. 255064 C. 250554 D. 255024
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育课上,20人一组进行足球比赛,每人射点球5次,已知某一组的进球总数为49个,进球情况记录如下表,其中进2个球的有x人,进3个球的有y人,若(x, y)恰好是两条直线的交点坐标,则这两条直线的解析式是( )

A. y=x+9与![]() B. y=-x+9与
B. y=-x+9与![]()
C. y=-x+9与![]() D. y=x+9与
D. y=x+9与![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是由若干个棱长为1cm的完全相同的小正方体组成的一个几何体.
(1)请画出这个几何体的三视图;

(2)在露出的表面上涂上颜色(不含底面),则涂上颜色部分的总面积为 cm2.
(3)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的三视图不变,那么最多可以再添加______个小正方体.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com