
【题目】如图,对称轴为直线x=2的抛物线经过点A(-1,0),C(0,5)两点,与x轴另一交点为B,已知M(0,1),E(a,0),F(a+1,0),点P是第一象限内的抛物线上的动点.
(1)求此抛物线的解析式;
(2)当a=1时,求四边形MEFP面积的最大值,并求此时点P的坐标;
(3)若△PCM是以点P为顶点的等腰三角形,求a为何值时,四边形PMEF周长最小?请说明理由.

【答案】(1)y=-x2+4x+5;(2)当![]() 时,四边形MEFP面积的最大,最大值为
时,四边形MEFP面积的最大,最大值为![]() ,此时点P坐标为
,此时点P坐标为![]() ;(3)当
;(3)当![]() 时,四边形FMEF周长最小.
时,四边形FMEF周长最小.
【解析】
试题(1)利用待定系数法求出抛物线的解析式;
(2)首先求出四边形MEFP面积的表达式,然后利用二次函数的性质求出最值及点P坐标;
(3)四边形PMEF的四条边中,PM、EF长度固定,因此只要ME+PF最小,则PMEF的周长将取得最小值.如答图3所示,将点M向右平移1个单位长度(EF的长度),得M1(1,1);作点M1关于x轴的对称点M2,则M2(1,﹣1);连接PM2,与x轴交于F点,此时ME+PF=PM2最小.
试题解析:方法一:
试题解析:(1)∵对称轴为直线x=2,
∴设抛物线解析式为y=a(x﹣2)2+k.
将A(﹣1,0),C(0,5)代入得:![]() ,解得
,解得![]() ,
,
∴y=﹣(x﹣2)2+9=﹣x2+4x+5.
(2)当a=1时,E(1,0),F(2,0),OE=1,OF=2.
设P(x,﹣x2+4x+5),
如答图2,过点P作PN⊥y轴于点N,则PN=x,ON=﹣x2+4x+5,
∴MN=ON﹣OM=﹣x2+4x+4.
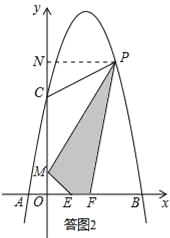
S四边形MEFP=S梯形OFPN﹣S△PMN﹣S△OME
=![]() (PN+OF)ON﹣
(PN+OF)ON﹣![]() PNMN﹣
PNMN﹣![]() OMOE
OMOE
=![]() (x+2)(﹣x2+4x+5)﹣
(x+2)(﹣x2+4x+5)﹣![]() x(﹣x2+4x+4)﹣
x(﹣x2+4x+4)﹣![]() ×1×1
×1×1
=﹣x2+![]() x+
x+![]()
=﹣(x﹣![]() )2+
)2+![]()
∴当x=![]() 时,四边形MEFP的面积有最大值为
时,四边形MEFP的面积有最大值为![]() ,
,
把x=![]() 时,y=﹣(
时,y=﹣(![]() ﹣2)2+9=
﹣2)2+9=![]() .
.
此时点P坐标为(![]() ,
,![]() ).
).
(3)∵M(0,1),C(0,5),△PCM是以点P为顶点的等腰三角形,
∴点P的纵坐标为3.
令y=﹣x2+4x+5=3,解得x=2±![]() .
.
∵点P在第一象限,∴P(2+![]() ,3).
,3).
四边形PMEF的四条边中,PM、EF长度固定,因此只要ME+PF最小,则PMEF的周长将取得最小值.
如答图3,将点M向右平移1个单位长度(EF的长度),得M1(1,1);
作点M1关于x轴的对称点M2,则M2(1,﹣1);
连接PM2,与x轴交于F点,此时ME+PF=PM2最小.

设直线PM2的解析式为y=mx+n,将P(2+![]() ,3),M2(1,﹣1)代入得:
,3),M2(1,﹣1)代入得:
![]() ,解得:m=
,解得:m=![]() ,n=﹣
,n=﹣![]() ,
,
∴y=![]() x﹣
x﹣![]() .
.
当y=0时,解得x=![]() .∴F(
.∴F(![]() ,0).
,0).
∵a+1=![]() ,∴a=
,∴a=![]() .
.
∴a=![]() 时,四边形PMEF周长最小.
时,四边形PMEF周长最小.
方法二:
(1)略.
(2)连接MF,过点P作x轴垂线,交MF于点H,
显然当S△PMF有最大值时,四边形MEFP面积最大.
当a=1时,E(1,0),F(2,0),
∵M(0,1),
∴lMF:y=﹣![]() x+1,
x+1,
设P(t,﹣t2+4t+5),H(t,﹣![]() t+1),
t+1),
∴S△PMF=![]() (PY﹣HY)(FX﹣MX),
(PY﹣HY)(FX﹣MX),
∴S△PMF=![]() (﹣t2+4t+5+
(﹣t2+4t+5+![]() t﹣1)(2﹣0)=﹣t2+
t﹣1)(2﹣0)=﹣t2+![]() t+4,
t+4,
∴当t=![]() 时,S△PMF最大值为
时,S△PMF最大值为![]() ,
,
∵S△MEF=![]() EF×MY=
EF×MY=![]() ×1×1=
×1×1=![]() ,
,
∴S四边形MEFP的最大值为![]() +
+![]() =
=![]() .
.
(3)∵M(0,1),C(0,5),△PCM是以点P为顶点的等腰三角形,
∴点P的纵坐标为3,∴﹣x2+4x+5=0,解得:x=2±![]() ,
,
∵点P在第一象限,∴P(2+![]() ,3),PM、EF长度固定,
,3),PM、EF长度固定,
当ME+PF最小时,PMEF的周长取得最小值,
将点M向右平移1个单位长度(EF的长度),得M1(1,1),
∵四边形MEFM1为平行四边形,
∴ME=M1F,
作点M1关于x轴的对称点M2,则M2(1,﹣1),
∴M2F=M1F=ME,
当且仅当P,F,M2三点共线时,此时ME+PF=PM2最小,
∵P(2+![]() ,3),M2(1,﹣1),F(a+1,0),
,3),M2(1,﹣1),F(a+1,0),
∴KPF=KM1F,∴![]() ,∴a=
,∴a=![]() .
.


科目:初中数学 来源: 题型:
【题目】去冬今春,我市部分地区遭受了罕见的旱灾,“旱灾无情人有情”.某单位给某乡中小学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件.
(1)求饮用水和蔬菜各有多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批饮用水和蔬菜全部运往该乡中小学.已知每辆甲种货车最多可装饮用水40件和蔬菜10件,每辆乙种货车最多可装饮用水和蔬菜各20件.则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来;
(3)在(2)的条件下,如果甲种货车每辆需付运费400元,乙种货车每辆需付运费360元.运输部门应选择哪种方案可使运费最少?最少运费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两组同时加工某种零件,乙组工作中有一次停产更换设备,更换设备后,乙组的工作效率是原来的2倍.两组各自加工零件的数量y(件)与时间x(时)的函数图象如图所示.
(1)直接写出甲组加工零件的数量y与时间x之间的函数关系式;
(2)求乙组加工零件总量a的值;
(3)甲、乙两组加工出的零件合在一起装箱,每满300件装一箱,零件装箱的时间忽略不计,求经过多长时间恰好装满第1箱?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展“我最喜爱的一项体育活动”调查,要求每名学生必选且只能选一项,现随机抽查了m名学生,并将其结果绘制成如下不完整的条形图和扇形图.

请结合以上信息解答下列问题:
(1)m= ;
(2)请补全上面的条形统计图;
(3)在图2中,“乒乓球”所对应扇形的圆心角的度数为 ;
(4)已知该校共有1200名学生,请你估计该校约有 名学生最喜爱足球活动.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC为⊙O的直径,B为⊙O上一点,∠ACB=30°,延长CB至点D,使得CB=BD,过点D作DE⊥AC,垂足E在CA的延长线上,连接BE.
(1)求证:BE是⊙O的切线;
(2)当BE=3时,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D、E、F分别为AB、BC、AC的中点,则下列结论:①△ADF≌△FEC;②四边形ADEF为菱形;③![]() 。其中正确的结论是____________.(填写所有正确结论的序号)
。其中正确的结论是____________.(填写所有正确结论的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
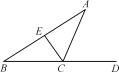
【题目】如图,CA平分∠DCE,且与BE的延长线相交于点A.
(1)若∠A=35°,∠B=30°,则∠BEC= ;(直接在横线上填写度数)
(2)小明经过改变∠A,∠B的度数进行多次探究,得出∠A,∠B,∠BEC三个角之间存在固定的数量关系,请你用一个等式表示出这个关系,并进行证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
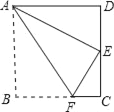
【题目】如图,四边形ABCD为平行四边形纸片.把纸片ABCD折叠,使点B恰好落在CD边上,折痕为AF.且AB=10cm、AD=8cm、DE=6cm.
(1)求证:平行四边形ABCD是矩形;
(2)求BF的长;
(3)求折痕AF长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次课外活动中,甲、乙两位同学测量公园中孔子塑像的高度,他们分别在A,B两处用高度为1.5m的测角仪测得塑像顶部C的仰角分别为30°,45°,两人间的水平距离AB为10m,求塑像的高度CF.(结果保留根号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com