
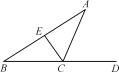
【题目】如图,CA平分∠DCE,且与BE的延长线相交于点A.
(1)若∠A=35°,∠B=30°,则∠BEC= ;(直接在横线上填写度数)
(2)小明经过改变∠A,∠B的度数进行多次探究,得出∠A,∠B,∠BEC三个角之间存在固定的数量关系,请你用一个等式表示出这个关系,并进行证明.
【答案】(1)100°;(2)∠BEC=2∠A+∠B,理由见解析
【解析】
(1)依据三角形外角性质,即可得到∠ACD=∠A+∠B=65°,依据AC平分∠DCE,可得∠ACE=∠ACD=65°,进而得出∠BEC=∠A+∠ACE=35°+65°=100°;
(2)依据AC平分∠DCE,可得∠ACD=∠ACE,依据三角形外角性质可得∠BEC=∠A+∠ACE=∠A+∠ACD,根据∠ACD=∠A+∠B,即可得到∠BEC=∠A+∠A+∠B=2∠A+∠B.
(1)∵∠A=35°,∠B=30°,
∴∠ACD=∠A+∠B=65°,
又∵AC平分∠DCE,
∴∠ACE=∠ACD=65°,
∴∠BEC=∠A+∠ACE=35°+65°=100°,
故答案为:100°;
解:∠BEC=2∠A+∠B.
证明:∵CA平分∠DCE,
∴∠ACD=∠ACE.
∵∠BEC=∠A+∠ACE=∠A+∠ACD,
∠ACD=∠A+∠B,
∴∠BEC=∠A+∠A+∠B=2∠A+∠B.


科目:初中数学 来源: 题型:
【题目】请阅读下列材料,并完成相应的任务:
在数学中,利用图形在变化过程中的不变性质,常常可以找到解决问题的办消去.著名美籍匈牙利数学家波利亚在他所著的《数学的发现》一书中有这样一个例子:请问如何在一个三角形ABC的AC和BC两边上分别取一点X和Y,使得AX=BY=XY.(如图)解决这个问题的操作步骤如下:
第一步,在CA上作出一点D,使得CD=CB,连接BD.第二步,在CB上取一点Y',作Y'Z∥CA,交BD于点Z',并在AB上取一点A',使Z'A'=Y'Z'.第三步,过点A作AZ∥A'Z',交BD于点Z.第四步,过点Z作ZY∥AC,交BC于点Y,再过点Y作YX∥ZA,交AC于点X.
则有AX=BY=XY.
下面是该结论的部分证明:
证明:∵AZ∥A'Z',∴∠BA'Z'=∠BAZ,
又∵∠A'BZ'=∠ABZ.∴△BA'Z'~△BAZ.
∴![]() .
.
同理可得![]() .∴
.∴![]() .
.
∵Z'A'=Y'Z',∴ZA=YZ.

在数学中,利用图形在变化过程中的不变性质,常常可以找到解决问题的办消去.著名美籍匈牙利数学家波利亚在他所著的《数学的发现》一书中有这样一个例子:请问如何在一个三角形ABC的AC和BC两边上分别取一点X和Y,使得AX=BY=XY.(如图)解决这个问题的操作步骤如下:
第一步,在CA上作出一点D,使得CD=CB,连接BD.第二步,在CB上取一点Y',作Y'Z∥CA,交BD于点Z',并在AB上取一点A',使Z'A'=Y'Z'.第三步,过点A作AZ∥A'Z',交BD于点Z.第四步,过点Z作ZY∥AC,交BC于点Y,再过点Y作YX∥ZA,交AC于点X.
则有AX=BY=XY.
下面是该结论的部分证明:
证明:∵AZ∥A'Z',∴∠BA'Z'=∠BAZ,
又∵∠A'BZ'=∠ABZ.∴△BA'Z'~△BAZ.
∴![]() .
.
同理可得![]() .∴
.∴![]() .
.
∵Z'A'=Y'Z',∴ZA=YZ.

任务:(1)请根据上面的操作步骤及部分证明过程,判断四边形AXYZ的形状,并加以证明;
(2)请再仔细阅读上面的操作步骤,在(1)的基础上完成AX=BY=XY的证明过程;
(3)上述解决问题的过程中,通过作平行线把四边形BA'Z'Y'放大得到四边形BAZY,从而确定了点Z,Y的位置,这里运用了下面一种图形的变化是 .
A.平移 B.旋转 C.轴对称 D.位似
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过A(﹣1,0),B(4,0),C(0,3)三点,D为直线BC上方抛物线上一动点,DE⊥BC于E.

(1)求抛物线的函数表达式;
(2)如图1,求线段DE长度的最大值;
(3)如图2,设AB的中点为F,连接CD,CF,是否存在点D,使得△CDE中有一个角与∠CFO相等?若存在,求点D的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对称轴为直线x=2的抛物线经过点A(-1,0),C(0,5)两点,与x轴另一交点为B,已知M(0,1),E(a,0),F(a+1,0),点P是第一象限内的抛物线上的动点.
(1)求此抛物线的解析式;
(2)当a=1时,求四边形MEFP面积的最大值,并求此时点P的坐标;
(3)若△PCM是以点P为顶点的等腰三角形,求a为何值时,四边形PMEF周长最小?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
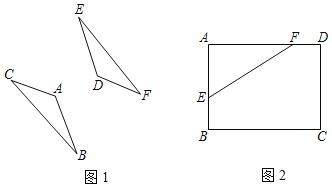
【题目】尺规作图,不写作法,保留作图痕迹
(1)如图1,若△ABC与△DEF关于直线l对称,请作出直线l;
(2)如图2,在矩形ABCD中,已知点B,F分别在AD和AB上,请在边BC上作出点G,在边CD作出点H,使得四边形FEGH的周长最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,按下列步骤作图:①以点B为圆心,适当长为半径画弧,与AB,BC分别交于点D,E;②分别以D,E为圆心,大于![]() DE的长为半径画弧,两弧交于点P;③作射线BP交AC于点F;④过点F作FG⊥AB于点G.下列结论正确的是( )
DE的长为半径画弧,两弧交于点P;③作射线BP交AC于点F;④过点F作FG⊥AB于点G.下列结论正确的是( )
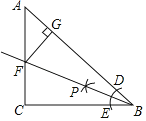
A. CF=FG B. AF=AG C. AF=CF D. AG=FG
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)图象的一部分如图所示,对称轴为x=![]() ,且经过点(2,0).下列结论:①ac<0;②4a+2b+c<0;③a-b+c=0;④若(-2,y1),(-3,y2)是抛物线上的两点,则y1<y2.其中正确结论的个数是( )
,且经过点(2,0).下列结论:①ac<0;②4a+2b+c<0;③a-b+c=0;④若(-2,y1),(-3,y2)是抛物线上的两点,则y1<y2.其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com