
һ�������ĺ���װ�����ɸ�ֻ����ɫ��ͬ�ĺ��������
��1����������2�������2����������������������ǡ����һ��һ�ĸ����Ƕ��٣����û���״ͼ���б��ķ�ʽ˵����
��2�����ȴӺ�������8�����ϼǺŷŻغ��У��ٽ�������ʵ�飮����ʵ���Ҫ��ÿ������ǰ�Ƚ�����ȣ�����һ����¼��ɫ��Żغ��У��ټ�����һ������50�Σ�ͳ�ƽ�����±���
| �����ɫ | �Ǻ� | �мǺ� | ||
| ��ɫ | ��ɫ | ��ɫ | ��ɫ | |
| �����Ĵ��� | 18 | 28 | 2 | 2 |
������������ʵ��Ľ���ɹ�����к������ռ�������İٷ�֮����
��3���ڣ�2���������¹�����к���ĸ�����
�����㡿�б�������״ͼ��������Ƶ�ʹ��Ƹ��ʣ�
����������1�����ȸ������⻭����״ͼ��Ȼ������״ͼ������еȿ��ܵĽ���������������������ǡ����һ��һ������������ø��ʹ�ʽ������ô𰸣�
��2�����������50������ʵ���У����ֺ���20�Σ�����30�Σ��̶���ô𰸣�
��3���������֪��50������ʵ���У������мǺŵ���4�Σ��������������̶���ô𰸣�
����𡿽⣺��1������״ͼ�ã�
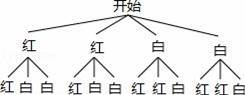

�߹���12�ֵȿ��ܵĽ����������������������ǡ����һ��һ����8�������
��P��ǡ����һ��һ�ף�=
 =
=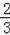
 ��
��
��2���������֪��50������ʵ���У����ֺ���20�Σ�����30�Σ�
�������ռ�ٷֱ�Ϊ20��50=40%��
������ռ�ٷֱ�Ϊ30��50=60%��
�𣺺���ռ40%������ռ60%��
��3���������֪��50������ʵ���У������мǺŵ���4�Σ�
��������Ϊ8��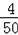
 =100��
=100��
�������Ϊ100��40%=40��
�𣺺��к�����40����
��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ���ڡ�ABC�У�AB=AC=13���ף�BC=10���ף�AD��BC�ڵ�D������P�ӵ�A������ÿ��1�����ٶ����߶�AD�����յ�D�˶����趯���˶�ʱ��Ϊt�룮

��1����AD�ij���
��2������PDC�����Ϊ15ƽ������ʱ�� ��t��ֵ��
��t��ֵ��
��3������M�ӵ�C������ÿ��2�����ٶ�������CB���˶�����M���Pͬʱ�������ҵ���P�˶����յ�Dʱ����MҲֹͣ�˶����Ƿ����t��ʹ��S��PMD= S��ABC�������ڣ������t��ֵ���������ڣ���˵�����ɣ�
S��ABC�������ڣ������t��ֵ���������ڣ���˵�����ɣ�
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
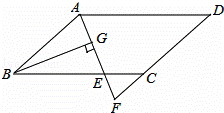
��ͼ����ƽ���ı���ABCD�У�AB=6��AD=9����BAD��ƽ���߽�BC��
��E����DC���ӳ����ڵ�F��BG��AE��G��BG=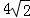 ��������AECD��
��������AECD��
�ܳ�������
�� A��22 B��23 C��24 D��25
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
ijУ�ڿ�չ�� ���ҵ��й��Ρ�Ϊ������ݽ������У���9��ѧ���μӱ��������Ǿ��������ճɼ�������ͬ�����е�һ��ѧ��Ҫ��֪���Լ��ܷ����ǰ5��������Ҫ�˽��Լ��ijɼ�����Ҫ�˽���9��ѧ���ɼ��ģ�������
�� A������ B������ C��ƽ���� D����λ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ����֪�ı���ABCD�DZ߳�Ϊ2�������Σ��ԶԽ���BDΪ������������BDE����E��DA���ӳ��ߵĴ���EF������ΪF��
��1���ҳ�ͼ����EF��ȵ��߶Σ���֤����Ľ��ۣ�
��2����AF�ij���


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��˫��С˫�������깺��һ�ű������˻����Ʊ���ֵ��������ֱ��ñ��������ҳ���������û�������κ������С�������һ����Ϸȷ��˭ȥ��
��˫��A���з��ŷֱ��������1��2��3������С��B���з��ŷֱ��������4��5������С���Ҷ��Ѹ��Խ��ȣ�С˫�����۾��������ڴ��и�ȡ��1��С��������С���ϵ�����֮��Ϊż�������˫�õ���Ʊ������Ϊ��������С˫�õ���Ʊ��
С˫���ڴ��з��ŷֱ��������1��2��3������С�����ѽ��ȣ���˫��С˫�������۾��зŻص���1�Σ���˫����ż���ͼ�2�֣�����������0�֣�С˫���������ͼ�1�֣�����ż����0�֣����ֶ�ľ͵õ���Ʊ������������ͬ�����ظ��ڶ��Σ���
��1����˫��Ƶ���Ϸ������˫���Ƿ�ƽ�����������б�����״ͼ˵�����ɣ�
��2��С˫��Ƶ���Ϸ������˫���Ƿ�ƽ������˵����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com