Question

在直角坐标平面内，二次函数图象的经过A（-1，0）、B（3，0），且过点C（0，3）．
（1）求该二次函数的解析式；
（2）若P是该抛物线上一点，且△ABC与△ABP面积相同，求P的坐标．

Answer 1

解：（1）∵二次函数图象的经过A（-1，0）、B（3，0），
∴设该二次函数的解析式是y=a（x+1）（x-3），
∵过点C（0，3），
∴代入得：3=a（0+1）（0-3），
a=-1，
∴该二次函数的解析式是y=-（x+1）（x-3），即y=-x²+2x+3．

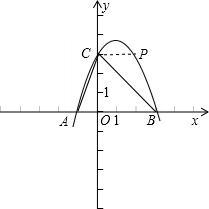
（2）∵P是该抛物线上一点，且△ABC与△ABP面积相同，
∴△ACB的边AB上的高和△ABP的边AB上的高相等，都是C点的纵坐标3，
即当P在x轴的上方时，P的纵坐标是3，
把y=3代入y=-x²+2x+3得：-x²+2x+3=3，
解得：x₁=0，x₂=2，
∵C（0，3），
∴P（2，3）；
当当P在x轴的下方时，P的纵坐标是-3，
把y=-3代入y=-x²+2x+3得：-x²+2x+3=-3，
解得：x₁=1+，x₂=1-，
∵C（0，3），
∴P（1+，-3），（1-，-3）；
即符合条件的P点的坐标是（2，3）或（1+，-3）或（1-，-3）．
分析：（1）设该二次函数的解析式是y=a（x+1）（x-3），把点C（0，3）代入求出即可；
（2）根据三角形面积和C的坐标，即可得出P的纵坐标式3或-3，把y=3和y=-3分别代入二次函数的解析式求出即可．
点评：本题考查了用待定系数法求二次函数的解析式，三角形面积的应用，用了分类讨论思想．