
����Ŀ���ۺ���
��1������
��ͼ���� ![]() Ϊ�߶�
Ϊ�߶� ![]() ��һ���㣬��
��һ���㣬�� ![]() ��
�� ![]() .
.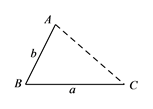
��գ����� ![]() λ��ʱ���߶�
λ��ʱ���߶� ![]() �ij�ȡ�����ֵ�������ֵΪ.���ú�
�ij�ȡ�����ֵ�������ֵΪ.���ú� ![]() ��
�� ![]() ��ʽ�ӱ�ʾ��
��ʽ�ӱ�ʾ��
��2��Ӧ��
�� ![]() Ϊ�߶�
Ϊ�߶� ![]() ��һ���㣬��
��һ���㣬�� ![]() ��
�� ![]() .��ͼ��ʾ���ֱ���
.��ͼ��ʾ���ֱ��� ![]() ��
�� ![]() Ϊ�ߣ����ȱ�������
Ϊ�ߣ����ȱ������� ![]() �͵ȱ�������
�͵ȱ������� ![]() ������
������ ![]() ��
�� ![]() .
.
���ҳ�ͼ���� ![]() ��ȵ��߶Σ���˵�����ɣ�
��ȵ��߶Σ���˵�����ɣ�
��ֱ��д���߶� ![]() �������ֵ.
�������ֵ.
��3����չ
��ͼ����ƽ��ֱ������ϵ�У��� ![]() ������Ϊ
������Ϊ ![]() ����
���� ![]() ������Ϊ
������Ϊ ![]()
![]() Ϊ�߶�
Ϊ�߶� ![]() ��һ���㣬��
��һ���㣬�� ![]() ��
�� ![]() ��
�� ![]() �����߶�
�����߶� ![]() �������ֵ����ʱ��
�������ֵ����ʱ�� ![]() ������.
������.
���𰸡�
��1��CB���ӳ�����,a+b
��2���⣺��DC=BE,�������£�
�ߡ�ABD�͡�ACEΪ�ȱ������Σ�
��AD=AB,AC=AE,��BAD=��CAE=60�㣬
���BAD+��BAC=��CAE+��BAC������CAD=��EAB,
���CAD�ա�EAB.
��DC=BE.
��BE�����ֵ��4.
��3���⣺��ͼ3��
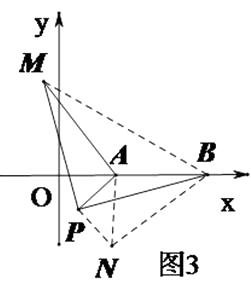
�����BNP�ա�MAP,��NB=AM,�ɣ�1��֪������N��BA���ӳ�����ʱ��NB�����ֵ���籸��ͼ����
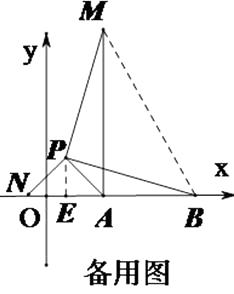
�á�APN�ǵ���ֱ�������Σ�AP=2����AN= ![]() ����AM=NB=AB+AN=3+
����AM=NB=AB+AN=3+ ![]() ;����P��PE��x���ڵ�E��PE=AE=
;����P��PE��x���ڵ�E��PE=AE= ![]() ,��A��2��0����P��2-
,��A��2��0����P��2- ![]() ��
�� ![]() ��
��
����������1������A���߶�CB���ӳ�����ʱ���ɵ��߶�AC�ij�ȡ�����ֵΪa+b��
��1�����ݵ�Aλ��CB���ӳ�����ʱ���߶�AC�ij�ȡ�����ֵ�����ɵõ����ۡ�
��2���ٸ��ݵȱ������ε����ʵõ�AD=AB��AC=AE����BAD=��CAE=60�㣬�Ƴ���CAD�ա�EAB������ȫ�������ε����ʵõ�CD=BE���������߶�BE�������ֵ=�߶�CD�����ֵ�����ݣ�1���еĽ��ۼ��ɵõ������
��3������BM������APM���ŵ�P˳ʱ����ת90��õ���PBN������AN���õ���APN�ǵ���ֱ�������Σ�����ȫ�������ε����ʵ�PN=PA=2��BN=AM�����ݵ�N���߶�BA���ӳ���ʱ���߶�BNȡ�����ֵ�����ɵõ����ֵ����ͼ2����P��PE��x����E�����ݵ���ֱ�������ε����ʼ��ɵõ����ۣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʹ��x2+px+8����x2��3x+q���˻��в���x2��x3���p��q��ֵ�ǣ� ��
A.p=0��q=0
B.p=3��q=1
C.p=��3��q=��9
D.p=��3��q=1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�� ![]() ��һ��
��һ�� ![]() Ϊƽ�澵��
Ϊƽ�澵�� ![]() ����
���� ![]() ����һ��
����һ�� ![]() ����
���� ![]() �����һ�����߾�
�����һ�����߾� ![]() ��һ��
��һ�� ![]() ���䣬�������
���䣬������� ![]() ǡ����
ǡ���� ![]() ƽ�У���
ƽ�У��� ![]() �Ķ����ǣ� ��
�Ķ����ǣ� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�A��B�ֱ�Ϊx�ᡢy���������������㣬��BAO��ƽ�������OBA�����ƽ��������ֱ�߽��ڵ�C�����C�Ķ�����A��B�˶��ı仯�����ȷ���ǣ� ��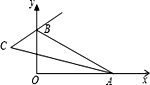
A.��B�������ڵ�A�����˶��Ĺ����У���C�Ķ�����С
B.��A�������ڵ�B�����˶��Ĺ����У���C�Ķ�����С
C.�ڵ�A�����˶�����B�����˶��Ĺ����У���C�Ķ���������
D.�ڵ�A��B�˶��Ĺ����У���C�Ķ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ�κ��ʱ�ڵ���ѧ�����մ���������Բ��������ΪԲ�ڽ�������α�����������ʱ���ܳ���Խ�ӽ�Բ�ܳ����ɴ������Բ����![]() �Ľ���ֵ����뾶Ϊ
�Ľ���ֵ����뾶Ϊ![]() ��Բ�ڽ���
��Բ�ڽ���![]() ���ε��ܳ�Ϊ
���ε��ܳ�Ϊ![]() ��Բ��ֱ��Ϊ
��Բ��ֱ��Ϊ![]() ������ͼ��ʾ����
������ͼ��ʾ����![]() ʱ��
ʱ��![]() ����ô��
����ô��![]() ʱ��
ʱ��![]() ���������ȷ��
���������ȷ��![]() ���ο����ݣ�
���ο����ݣ�![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������10�֣�
��ͼ��������![]() ������
������![]() ��
��![]() ��ֱ��
��ֱ��![]()
![]() ��
��![]() ���ڵ�
���ڵ�![]() �����������߽���
�����������߽���![]() ��
��![]() ���㣮
���㣮![]() Ϊ��������һ���㣨����
Ϊ��������һ���㣨����![]() ��
��![]() �غϣ���
�غϣ���
��1���������ߵĽ���ʽ��
��2������![]() ��ֱ��
��ֱ��![]() �·�ʱ������
�·�ʱ������![]() ��
��![]() �ύ
�ύ![]() �ڵ�
�ڵ�![]() ��
��![]() �ύ
�ύ![]() �ڵ�
�ڵ�![]() ����
����![]() �����ֵ��
�����ֵ��
��3����![]() Ϊֱ��
Ϊֱ��![]() �ϵĵ㣬��
�ϵĵ㣬��![]() ��
��![]() ��
��![]() ��
��![]() Ϊ������ı����ܷ�ƽ���ı��Σ����ܣ������
Ϊ������ı����ܷ�ƽ���ı��Σ����ܣ������![]() �����ꣻ�����ܣ���˵�����ɣ�
�����ꣻ�����ܣ���˵�����ɣ�
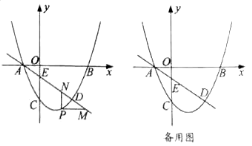
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������8�֣�
��ͼ��ֱ��![]() ��˫����
��˫����![]() ��
��![]() ������
Ϊ������![]() ���ڵ�һ�����ڽ��ڵ�
���ڵ�һ�����ڽ��ڵ�![]() ������
������![]() �ᡢ
�ᡢ![]() ��ֱ���
��ֱ���![]() ��
��![]() ���㣮
���㣮
��1����ֱ�ߺ�˫���ߵĽ���ʽ��
��2����![]() ��
��![]() ���ϣ���
���ϣ���![]() ���������
���������![]() ����
����![]() ������꣮
������꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵������ȷ���ǣ� ��
A.��ij����˶�Ա���һ�Σ����а��ġ���������¼�
B.��13��ͬѧ����������ͬѧ�ij����·�����ͬ�ġ����ڱ�Ȼ�¼�
C.���ڱ�����ѹ�£����¶Ƚ���-5��ʱ��ˮ��ɱ�����������¼�
D.��ij������8���ʵؾ��ȵ����Ҷ��Ǻ�����������һ���ǰ������ڲ������¼�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com