
【题目】(本题满分8分)
如图,直线![]() 与双曲线
与双曲线![]() (
(![]() 为常数,
为常数,![]() )在第一象限内交于点
)在第一象限内交于点![]() ,且与
,且与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点.
两点.
(1)求直线和双曲线的解析式;
(2)点![]() 在
在![]() 轴上,且
轴上,且![]() 的面积等于
的面积等于![]() ,求
,求![]() 点的坐标.
点的坐标.

【答案】(1)直线的解析式为y=x+1;双曲线的解析式为y=![]() ;(2)P点的坐标为(3,0)或(-5,0).
;(2)P点的坐标为(3,0)或(-5,0).
【解析】
试题分析:(1)把A(1,2)代入双曲线以及直线y=x+b,分别可得k,b的值;
(2)先根据直线解析式得到BO=CO=1,再根据△BCP的面积等于2,即可得到P的坐标.
试题解析:(1)把A(1,2)代入双曲线y=![]() ,可得k=2,
,可得k=2,
∴双曲线的解析式为y=![]() ;
;
把A(1,2)代入直线y=x+b,可得b=1,
∴直线的解析式为y=x+1;
(2)设P点的坐标为(x,0),
在y=x+1中,令y=0,则x=-1;令x=0,则y=1,
∴B(-1,0),C(0,1),即BO=1=CO,
∵△BCP的面积等于2,
∴![]() BP×CO=2,即
BP×CO=2,即![]() |x-(-1)|×1=2,
|x-(-1)|×1=2,
解得x=3或-5,
∴P点的坐标为(3,0)或(-5,0).


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】综合题
(1)发现
如图,点 ![]() 为线段
为线段 ![]() 外一动点,且
外一动点,且 ![]() ,
, ![]() .
.
填空:当点 ![]() 位于时,线段
位于时,线段 ![]() 的长取得最大值,且最大值为.(用含
的长取得最大值,且最大值为.(用含 ![]() ,
, ![]() 的式子表示)
的式子表示)
(2)应用
点 ![]() 为线段
为线段 ![]() 外一动点,且
外一动点,且 ![]() ,
, ![]() .如图所示,分别以
.如图所示,分别以 ![]() ,
, ![]() 为边,作等边三角形
为边,作等边三角形 ![]() 和等边三角形
和等边三角形 ![]() ,连接
,连接 ![]() ,
, ![]() .
.
①找出图中与 ![]() 相等的线段,并说明理由;
相等的线段,并说明理由;
②直接写出线段 ![]() 长的最大值.
长的最大值.
(3)拓展
如图,在平面直角坐标系中,点 ![]() 的坐标为
的坐标为 ![]() ,点
,点 ![]() 的坐标为
的坐标为 ![]()
![]() 为线段
为线段 ![]() 外一动点,且
外一动点,且 ![]() ,
, ![]() ,
, ![]() ,求线段
,求线段 ![]() 长的最大值及此时点
长的最大值及此时点 ![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰△ABC中,AC=BC,以BC为直径的⊙O分别与AB,AC相交于点D,E,过点D作DF⊥AC,垂足为点F.
(1)求证:DF是⊙O的切线;
(2)分别延长CB,FD,相交于点G,∠A=60°,⊙O的半径为6,求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用“☆”定义一种新运算:对于任意有理数a和b,规定a☆b=ab2﹣2ab+b.如:2☆(﹣3)=2×(﹣3)2﹣2×2×(﹣3)+(﹣3)=27.依据此定义化简(1﹣3x)☆(﹣4)=____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图像与
的图像与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,
,![]() .点
.点![]() 在函数图像上,
在函数图像上,![]() 轴,且
轴,且![]() ,直线
,直线![]() 是抛物线的对称轴,
是抛物线的对称轴,![]() 是抛物线的顶点.
是抛物线的顶点.
(1)求![]() 、
、![]() 的值;
的值;
(2)如图①,连接![]() ,线段
,线段![]() 上的点
上的点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 恰好在线段
恰好在线段![]() 上,求点
上,求点![]() 的坐标;
的坐标;
(3)如图②,动点![]() 在线段
在线段![]() 上,过点
上,过点![]() 作
作![]() 轴的垂线分别与
轴的垂线分别与![]() 交于点
交于点![]() ,与抛物线交于点
,与抛物线交于点![]() .试问:抛物线上是否存在点
.试问:抛物线上是否存在点![]() ,使得
,使得![]() 与
与![]() 的面积相等,且线段
的面积相等,且线段![]() 的长度最小?如果存在,求出点
的长度最小?如果存在,求出点![]() 的坐标;如果不存在,说明理由.
的坐标;如果不存在,说明理由.
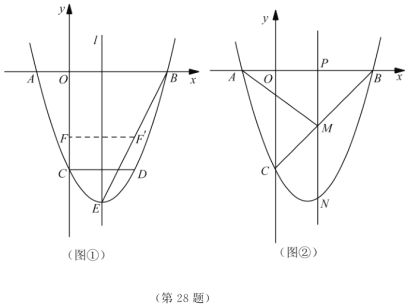
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com