
 如图所示,直线AB、CD相交于点O,OM⊥AB.
如图所示,直线AB、CD相交于点O,OM⊥AB.分析 (1)根据垂直定义可得∠AOM=90°,进而可得∠1+∠AOC=90°,再利用等量代换可得到∠2+∠AOC=90°,从而可得ON⊥CD;
(2)根据垂直定义和条件可得∠1=30°,∠BOC=120°,再根据邻补角定义可得∠MOD的度数.
解答 解:(1)ON⊥CD.
理由如下:
∵OM⊥AB,
∴∠AOM=90°,
∴∠1+∠AOC=90°,
又∵∠1=∠2,
∴∠2+∠AOC=90°,
即∠CON=90°,
∴ON⊥CD.
(2)∵OM⊥AB,$∠1=\frac{1}{4}$∠BOC,
∴∠1=30°,∠BOC=120°,
又∵∠1+∠MOD=180°,
∴∠MOD=180°-∠1=150°.
点评 此题主要垂直定义,关键是掌握垂线的定义当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图1为放置在水平桌面上的台灯的平面示意图,灯臂AO长为50cm,与水平桌面所形成的夹角∠OAM为75°.由光源O射出的边缘光线OC,OB与水平桌面所形成的夹角∠OCA,∠OBA分别为90°和30°.(不考虑其他因素,结果精确到0.1cm. sin75°≈0.97,cos75°≈0.26,$\sqrt{3}$≈1.73
如图1为放置在水平桌面上的台灯的平面示意图,灯臂AO长为50cm,与水平桌面所形成的夹角∠OAM为75°.由光源O射出的边缘光线OC,OB与水平桌面所形成的夹角∠OCA,∠OBA分别为90°和30°.(不考虑其他因素,结果精确到0.1cm. sin75°≈0.97,cos75°≈0.26,$\sqrt{3}$≈1.73查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1000}{x-100}$-$\frac{1000}{x}$=10 | B. | $\frac{1000}{x}$=$\frac{1000}{x+100}$+10 | ||
| C. | $\frac{1000}{x}$=$\frac{1000}{x-100}$+10 | D. | $\frac{1000}{x+100}$-$\frac{1000}{x}$=10 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 求两个有理数的绝对值,并比较大小 | |
| B. | 确定和的符号 | |
| C. | 观察两个有理数的符号,并作出一些判断 | |
| D. | 用较大的绝对值减去较小的绝对值 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
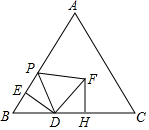 如图,在等边△ABC中,AB=10,BD=4,BE=2,点P从点E出发沿EA方向运动,连接PD,以PD为边,在PD右侧按如图方式作等边△DPF.
如图,在等边△ABC中,AB=10,BD=4,BE=2,点P从点E出发沿EA方向运动,连接PD,以PD为边,在PD右侧按如图方式作等边△DPF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com