
 如图1为放置在水平桌面上的台灯的平面示意图,灯臂AO长为50cm,与水平桌面所形成的夹角∠OAM为75°.由光源O射出的边缘光线OC,OB与水平桌面所形成的夹角∠OCA,∠OBA分别为90°和30°.(不考虑其他因素,结果精确到0.1cm. sin75°≈0.97,cos75°≈0.26,$\sqrt{3}$≈1.73
如图1为放置在水平桌面上的台灯的平面示意图,灯臂AO长为50cm,与水平桌面所形成的夹角∠OAM为75°.由光源O射出的边缘光线OC,OB与水平桌面所形成的夹角∠OCA,∠OBA分别为90°和30°.(不考虑其他因素,结果精确到0.1cm. sin75°≈0.97,cos75°≈0.26,$\sqrt{3}$≈1.73分析 (1)在直角三角形ACO中,根据sin75°=$\frac{OC}{OA}$,求出OC,在直角三角形BCO中,tan30°=$\frac{OC}{BC}$,求出BC即可.
(2)如图,过点P作PH⊥AB于H,交OB于M,过点D作DG⊥PH于G,DQ⊥AB于Q,则四边形DGHQ为矩形,∠GDF=∠EFC=∠DPG=60°,求出PH,MH的长即可判断.
解答 解:(1)在直角三角形ACO中,sin75°=$\frac{OC}{OA}$,
解得OC=50×0.97≈48.5,
在直角三角形BCO中,tan30°=$\frac{OC}{BC}$,
解得BC=1.73×48.5≈83.9.
答:该台灯照亮水平面的宽度BC大约是83.9cm,
(2)如图,过点P作PH⊥AB于H,交OB于M,过点D作DG⊥PH于G,DQ⊥AB于Q,则四边形DGHQ为矩形,∠GDF=∠EFC=∠DPG=60°
由题意DE=DF=12,DP=34,
∴PG=17,QH=DG=17$\sqrt{3}$,QF=6,GH=DQ=6$\sqrt{3}$,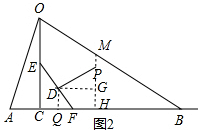
∴PH=PH+GH=17+6$\sqrt{3}$≈27.38,
又∵CH=6+17$\sqrt{3}$≈35.41
∴HB=CB-CH=83.9-35.41≈48.49,
∵∠OBC=30°,tan∠OBC=1:$\sqrt{3}$,
∴MH=HB÷$\sqrt{3}$=48.49÷$\sqrt{3}$≈28.03,
∵27.38<28.03,
∴最佳视点P在灯光照射范围内.
点评 本题考查解直角三角形的应用、线段的垂直平分线的性质、视点、盲点和盲区等知识,解题的关键是灵活应用所学知识解决问题,属于中考常考题型.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:解答题
 春天来了,小明骑自行车从家里出发到野外郊游,从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地,小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍.
春天来了,小明骑自行车从家里出发到野外郊游,从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地,小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,⊙O 的半径为1,PA,PB是⊙O的两条切线,切点分别为A,B.连接OA,OB,AB,PO,若∠APB=60°,则△PAB的周长为3$\sqrt{3}$.
如图,⊙O 的半径为1,PA,PB是⊙O的两条切线,切点分别为A,B.连接OA,OB,AB,PO,若∠APB=60°,则△PAB的周长为3$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,直线AB、CD相交于点O,OM⊥AB.
如图所示,直线AB、CD相交于点O,OM⊥AB.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com