
【题目】对于平面直角坐标系![]() 中的点
中的点![]() ,若
,若![]() ,
,![]() 满足
满足![]() ,则点
,则点![]() 就称为“绝好点”.例如:
就称为“绝好点”.例如:![]() ,因为
,因为![]() ,所以
,所以![]() 是“绝好点”.
是“绝好点”.
(1)点![]() “绝好点”;点
“绝好点”;点![]() “绝好点”(填“是”或“不是);
“绝好点”(填“是”或“不是);
(2)已知一次函数![]() (
(![]() 为常数)图像上有一个“绝好点”的坐标是
为常数)图像上有一个“绝好点”的坐标是![]() ,一次函数
,一次函数![]() (
(![]() 为常数)图像上是否存在其他“绝好点”?若存在,请求出来;若不存在,请说明理由;
为常数)图像上是否存在其他“绝好点”?若存在,请求出来;若不存在,请说明理由;
(3)点![]() 和点
和点![]() 为一次函数
为一次函数![]() (
(![]() 为常数且
为常数且![]() )图像上的两个“绝好点”,点
)图像上的两个“绝好点”,点![]() 在
在![]() 轴上运动,当
轴上运动,当![]() 最小时,求点
最小时,求点![]() 的坐标.(用含字母
的坐标.(用含字母![]() 的式子表示)
的式子表示)
【答案】(1)是;不是;(2)存在,其他“绝好点”为![]() ;(3)点
;(3)点![]() 为
为![]() .
.
【解析】
(1)根据“绝好点”的定义即可判断;
(2)先把![]() 代入
代入![]() 求出m,得到
求出m,得到![]() ,再根据“绝好点”的定义得到
,再根据“绝好点”的定义得到![]() ,再分情况讨论即可求解;
,再分情况讨论即可求解;
(3)由题意得“绝好点”在函数![]() 或
或![]() 图像上,分情况分别求出A,B的坐标,再得到点
图像上,分情况分别求出A,B的坐标,再得到点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,求出直线A’B的解析式,再求出其与x轴的交点即可.
,求出直线A’B的解析式,再求出其与x轴的交点即可.
(1)∵![]() ,
,![]()
∴点![]() 是“绝好点”, 点
是“绝好点”, 点![]() 不是“绝好点”;
不是“绝好点”;
故答案为:是;不是;
(2)将点坐标![]() 代入
代入![]() 得:
得:
![]() ;∴
;∴![]() ,∴
,∴![]()
又∵![]() ,∴
,∴![]() 或
或![]()
①当![]() 时
时
联立得:![]()
解得![]() 代入得
代入得![]()
所以![]() 为其本身
为其本身
②当![]() 时
时
联立得:![]()
解得![]() 代入得
代入得![]()
所以为另一个点坐标![]()
综上所述:存在其他“绝好点”为![]()
(3)由题意得“绝好点”在函数![]() 或
或![]() 图像上
图像上
①当在函数![]() 上时,
上时,
![]()
解得![]()
代入得![]() ,
,
∴![]() 为
为![]()
②当在函数![]() 上时,
上时,
![]()
解得![]()
代入得![]() ,
,
∴![]() 为
为![]()
∵![]() ,∴
,∴![]() ,
,![]() 都在第一象限.
都在第一象限.
点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]()
设直线A’B的解析式为y=kx+b
把点![]() 、
、![]() 代入得
代入得![]()
解得![]()
∴![]()
令![]() ,
,
解得![]() ;
;
∴点![]() 为
为![]() .
.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】某水果商贩用530元从批发市场购进桔子、苹果、香蕉、荔枝各100千克,并将这批水果全部售出,下图分别是桔子、苹果、荔枝售出后的总利润和四种水果售出的利润率,根据所给信息,下列结论:
①香蕉的进价为每千克1.50元;
②桔子的进价与苹果的进价一样;
③四种水果的销售额共有695元;
④若下一次进货时的进价与进货数量不变,且桔子、香蕉和荔枝的售价不变,要想四种水果的总利润为175元,则苹果的售价每千克应提高0.10元(![]() ).其中正确的结论是( )
).其中正确的结论是( )

A. ①②③
B. ①③④
C. ①④
D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
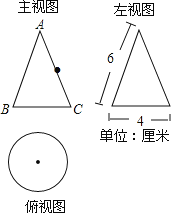
【题目】如图是一个几何体的三视图.
(1)写出该几何体的名称,并根据所示数据计算这个几何体的表面积;
(2)如果一只蚂蚁要从这个几何体中的点B出发,沿表面爬到AC的中点D,请你求出这个线路的最短路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
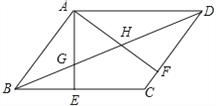
【题目】如图,在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,BD与AE、AF交于G、H.
(1)求证:△ABE∽△ADF;
(2)若AG=AH,求证:四边形ABCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一块直角三角形木板,它的一条直角边AB长1.5m,面积为1.5m2.甲、乙两位木匠分别按图①、②把它加工成一个正方形桌面.请说明哪个正方形面积较大(加工损耗不计).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 至
至![]() ,点
,点![]() 的对应点分别是
的对应点分别是![]() ,连接
,连接![]() 线段
线段![]() 与线段
与线段![]() 交于点M,连接
交于点M,连接![]() .
.
(1)如图1,求证:![]() ;
;
(2)如图1,求证:OM平分![]() ;
;
(3)如图2,若![]() ,求
,求![]() 的长.
的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两根长度为12米的绳子,一端系在旗杆上的同一位置A点,另一端分别固定在地面上的两个木桩B,C上(绳结处的误差忽略不计),现在只有一把卷尺,如何检验旗杆是否垂直于地面BC?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“一带一路”的进一歩推进,我国瓷器(“china”)更为“一带一路”沿践人民所推崇,一外国商户准这一商机,向我国一瓷器经销商咨询工艺品茶具,得到如下信息:
(1)每个茶壶的批发价比每个茶杯多120元;
(2)一套茶具包括一个茶壶与四个茶杯;
(3)4套茶具的批发价为1280元.
根据以上僖息:
(1)求每个茶壶与每个茶杯的批发价;
(2)若该商户购进茶杯的数量是茶壶数量的5倍还多18个,并且茶壶和茶杯的总数不超过320个,该商户计划将一半的茶具按每套500元成套销售,其余按每个茶壶300元,每个茶杯80元零售.没核商户购进茶壶m个.
①试用含m的关系式表示出该商户计划获取的利润;
②请帮助他设计一种获取利润最大的方案,并求出最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com