
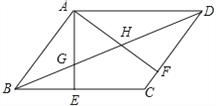
【题目】如图,在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,BD与AE、AF交于G、H.
(1)求证:△ABE∽△ADF;
(2)若AG=AH,求证:四边形ABCD是菱形.
【答案】(1)证明见解析;(2)菱形,证明见解析.
【解析】试题分析:(1)根据平行四边形的对角相等,以及垂直的定义可得△ABE和△ADF的两角对应相等,则两个三角形相似;
(2)证明△ABG≌△ADH,则AB=AD,从而证得四边形是菱形.
试题解析:(1)证明:∵AE⊥BC,AF⊥CD,
∴∠AEB=∠AFD=90°,
∵四边形ABCD是平行四边形,
∴∠ABE=∠ADF,
∴△ABE∽△ADF(有两角相等的三角形是相似三角形)
(2)∵△ABE∽△ADF,
∴∠BAG=∠DAH,
∵AG=AH,
∴∠AGH=∠AHG,
从而∠AGB=∠AHD,
∴△ABG≌△ADH(ASA),
∴AB=AD,
∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形(一组邻边相等的平行四边形是菱形)


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】快、慢两车分别从相距480千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,途中慢车因故停留1小时,然后以原速度继续向甲地行驶,到达甲地后停止行驶;快车到达乙地后,立即按原路原速返回甲地,(快车掉头的时间忽略不计),快、慢两车距乙地的路程y(千米)与所用时间x(小时)之间的函数图象如图.快车到达甲地时,慢车距离甲地__米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线MN∥PQ,直线AB分别与MN,PQ相交于点A,B.小宇同学利用尺规按以下步骤作图:①以点A为圆心,以任意长为半径作弧交AN于点C,交AB于点D;②分别以C,D为圆心,以大于![]() CD长为半径作弧,两弧在∠NAB内交于点E;③作射线AE交PQ于点F.若AB=2,∠ABP=60°,则线段AF的长为_____.
CD长为半径作弧,两弧在∠NAB内交于点E;③作射线AE交PQ于点F.若AB=2,∠ABP=60°,则线段AF的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲村至乙村的公路旁有一块山地正在开发,现有一![]() 处需要爆破.已知点
处需要爆破.已知点![]() 与公路上的停靠站
与公路上的停靠站![]() 的距离为
的距离为![]() 米,与公路上另一停靠站
米,与公路上另一停靠站![]() 的距离为
的距离为![]() 米,且
米,且![]() ,如图,为了安全起见,爆破点
,如图,为了安全起见,爆破点![]() 周围半径
周围半径![]() 米范围内不得进入,问在进行爆破时,公路
米范围内不得进入,问在进行爆破时,公路![]() 段是否有危险,是否需要暂时封锁?请通过计算进行说明.
段是否有危险,是否需要暂时封锁?请通过计算进行说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
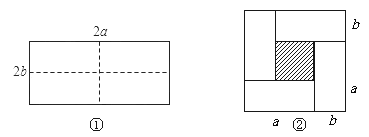
【题目】操作题
(1)如图①所示是一个长为2a,宽为2b的矩形,若把此图沿图中虚线用剪刀均分为四块小长方形,然后按图②的形状拼成一个正方形,请问:这两个图形的 不变.图②中阴影部分的面积用含a、b的代数式表示为_________________;
(2)由(1)的探索中,可得到的结论是:在周长一定的矩形中,___________时,面积最大;
(3)若一矩形的周长为36 cm,则当边长为多少时,该图形的面积最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 中的点
中的点![]() ,若
,若![]() ,
,![]() 满足
满足![]() ,则点
,则点![]() 就称为“绝好点”.例如:
就称为“绝好点”.例如:![]() ,因为
,因为![]() ,所以
,所以![]() 是“绝好点”.
是“绝好点”.
(1)点![]() “绝好点”;点
“绝好点”;点![]() “绝好点”(填“是”或“不是);
“绝好点”(填“是”或“不是);
(2)已知一次函数![]() (
(![]() 为常数)图像上有一个“绝好点”的坐标是
为常数)图像上有一个“绝好点”的坐标是![]() ,一次函数
,一次函数![]() (
(![]() 为常数)图像上是否存在其他“绝好点”?若存在,请求出来;若不存在,请说明理由;
为常数)图像上是否存在其他“绝好点”?若存在,请求出来;若不存在,请说明理由;
(3)点![]() 和点
和点![]() 为一次函数
为一次函数![]() (
(![]() 为常数且
为常数且![]() )图像上的两个“绝好点”,点
)图像上的两个“绝好点”,点![]() 在
在![]() 轴上运动,当
轴上运动,当![]() 最小时,求点
最小时,求点![]() 的坐标.(用含字母
的坐标.(用含字母![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
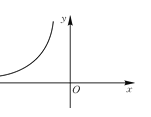
【题目】如图,反比例函数![]() 的图象的一支在平面直角坐标系中的位置如图所示,根据图象回答下列问题:
的图象的一支在平面直角坐标系中的位置如图所示,根据图象回答下列问题:
(1)图象的另一支在第 象限;在每个象限内,y随x的增大而 ;
(2)若此反比例函数的图象经过点(-2,3),求m的值.点A(-5,2)是否在这个函数图象上?点B(-3,4)呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,∠ABC=45°,AD是⊙O的切线交BC的延长线于D,AB交OC于E.

(1)求证:AD∥OC;
(2)若AE=2![]() ,CE=2.求⊙O的半径和线段BE的长.
,CE=2.求⊙O的半径和线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
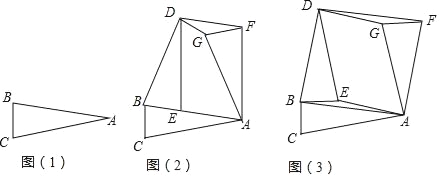
【题目】综合与实践
问题情境
在综合实践课上,老师让同学们“以三角形的旋转”为主题进行数学活动,如图(1),在三角形纸片ABC中,AB=AC,∠B=∠C=α.
操作发现
(1)创新小组将图(1)中的△ABC以点B为旋转中心,逆时针旋转角度α,得到△DBE,再将△ABC以点A为旋转中心,顺时针旋转角度α,得到△AFG,连接DF,得到图(2),则四边形AFDE的形状是 .
(2)实践小组将图(1)中的△ABC以点B为旋转中心,逆时针逆转90°,得到△DBE,再将△ABC以点A为旋转中心,顺时针旋转90°,得到△AFG,连接DF、DG、AE,得到图(3),发现四边形AFDB为正方形,请你证明这个结论.
拓展探索
(3)请你在实践小组操作的基础上,再写出图(3)中的一个特殊四边形,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com