
【题目】如图,![]() 为
为![]() 的高,
的高,![]() 为
为![]() 的角平分线,若
的角平分线,若![]() ,
,![]() .
.

(1)![]() ;
;
(2)求![]() 的度数;
的度数;
(3)若点![]() 为线段
为线段![]() 上任意一点,当
上任意一点,当![]() 为直角三角形时,则求
为直角三角形时,则求![]() 的度数.
的度数.
【答案】(1)26;(2)12°;(3)∠BFG的度数为58°或18°.
【解析】
(1)根据BF是∠ABC的角平分线且![]() ,可求出∠ABD,又
,可求出∠ABD,又![]() 为
为![]() 的高即可得出答案;
的高即可得出答案;
(2)根据∠AFB和∠ABF即可求出∠BAC,又AE是∠BAC的角平分线可求出∠BAE的度数,通过∠DAE=∠BAE-∠BAD即可得出答案;
(3)![]() 为直角三角形需要分情况讨论:①∠FGC=90°;②∠GFC=90°,针对以上两种情况分别求解.
为直角三角形需要分情况讨论:①∠FGC=90°;②∠GFC=90°,针对以上两种情况分别求解.
(1)∵BF是∠ABC的角平分线且![]()
∴∠ABF=32°∠ABD=64°
又![]() 为
为![]() 的高
的高
∴∠BAD=90°-∠ABD=26°
(2)∵![]() ,∠ABF=32°
,∠ABF=32°
∴∠BAC=180°-∠ABF-∠AFB=76°
又∵AE是∠BAC的角平分线
∴∠BAE=∠CAE=38°
∴∠DAE=∠BAE-∠BAD=12°
(3)在△ABC中,∠C=40°
∠BFC=180°-∠BFA=108°
当∠FGC=90°时,![]() 为直角三角形,此时∠CFG=50°
为直角三角形,此时∠CFG=50°
∴∠BFG=∠BFC-∠CFG=58°
当∠GFC=90°时,![]() 为直角三角形
为直角三角形
∴∠BFG=∠BFC-∠CFG=18°
综上,∠BFG的度数为58°或18°.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案科目:初中数学 来源: 题型:
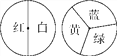
【题目】小明和小亮用如图所示的两个转盘做“配紫色”游戏,游戏规则是:分别转动两个转盘,若其中一个转盘转出红色,另一个转出蓝色,则可以配成紫色,此时小明得1分,否则小亮得1分.
(1)用画树状图或列表的方法求出小明获胜的概率;
(2)这个游戏对双方公平吗?请说明理由.若不公平,如何修改规则才能使游戏对双方公平?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A、B两地同时出发,甲车匀速前往B地,到达B地立即以另一速度按原路匀速返回到A地;乙车匀速前往A地,设甲、乙两车距A地的路程为y(千米),甲车行驶的时间为x(时),y与x之间的函数图象如图所示
(1)求甲车从A地到达B地的行驶时间;
(2)求甲车返回时y与x之间的函数关系式,并写出自变量x的取值范围;
(3)求乙车到达A地时甲车距A地的路程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲村至乙村的公路旁有一块山地正在开发,现有一![]() 处需要爆破.已知点
处需要爆破.已知点![]() 与公路上的停靠站
与公路上的停靠站![]() 的距离为
的距离为![]() 米,与公路上另一停靠站
米,与公路上另一停靠站![]() 的距离为
的距离为![]() 米,且
米,且![]() ,如图,为了安全起见,爆破点
,如图,为了安全起见,爆破点![]() 周围半径
周围半径![]() 米范围内不得进入,问在进行爆破时,公路
米范围内不得进入,问在进行爆破时,公路![]() 段是否有危险,是否需要暂时封锁?请通过计算进行说明.
段是否有危险,是否需要暂时封锁?请通过计算进行说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人在玩转盘游戏时,把转盘A、B分别分成4等份、3等份,并在每一份内标上数字,如图所示.游戏规定:转动两个转盘停止后,指针必须指到某一数字,否则重转.
(1)请用树状图或列表法列出所有可能的结果;
(2)若指针所指的两个数字都是方程x2-5x+6=0的解时,则甲获胜;若指针所指的两个数字都不是方程x2-5x+6=0的解时,则乙获胜,问他们两人谁获胜的概率大?请分析说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 中的点
中的点![]() ,若
,若![]() ,
,![]() 满足
满足![]() ,则点
,则点![]() 就称为“绝好点”.例如:
就称为“绝好点”.例如:![]() ,因为
,因为![]() ,所以
,所以![]() 是“绝好点”.
是“绝好点”.
(1)点![]() “绝好点”;点
“绝好点”;点![]() “绝好点”(填“是”或“不是);
“绝好点”(填“是”或“不是);
(2)已知一次函数![]() (
(![]() 为常数)图像上有一个“绝好点”的坐标是
为常数)图像上有一个“绝好点”的坐标是![]() ,一次函数
,一次函数![]() (
(![]() 为常数)图像上是否存在其他“绝好点”?若存在,请求出来;若不存在,请说明理由;
为常数)图像上是否存在其他“绝好点”?若存在,请求出来;若不存在,请说明理由;
(3)点![]() 和点
和点![]() 为一次函数
为一次函数![]() (
(![]() 为常数且
为常数且![]() )图像上的两个“绝好点”,点
)图像上的两个“绝好点”,点![]() 在
在![]() 轴上运动,当
轴上运动,当![]() 最小时,求点
最小时,求点![]() 的坐标.(用含字母
的坐标.(用含字母![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
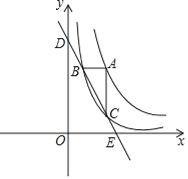
【题目】如图,点A在函数y=![]() (x>0)图象上,过点A作x轴和y轴的平行线分别交函数y=
(x>0)图象上,过点A作x轴和y轴的平行线分别交函数y=![]() 图象于点B,C,直线BC与坐标轴的交点为D,E.
图象于点B,C,直线BC与坐标轴的交点为D,E.
(1)当点C的横坐标为1时,求点B的坐标;
(2)试问:当点A在函数y=![]() (x>0)图象上运动时,△ABC的面积是否发生变化?若不变,请求出△ABC的面积,若变化,请说明理由.
(x>0)图象上运动时,△ABC的面积是否发生变化?若不变,请求出△ABC的面积,若变化,请说明理由.
(3)试说明:当点A在函数y=![]() (x>0)图象上运动时,线段BD与CE的长始终相等.
(x>0)图象上运动时,线段BD与CE的长始终相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应“低碳环保,绿色出行”的公益活动,小燕和妈妈决定周日骑自行车去图书馆借书.她们同时从家出发,小燕先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分钟的速度到达图书馆,而妈妈始终以120米/分钟的速度骑行,两人行驶的路程y(米)与时间x(分钟)的关系如图,请结合图像,解答下列问题:
(1)图书馆到小燕家的距离是 米;
(2)a= ,b= ,m= ;
(3)妈妈行驶的路程y(米)关于时间x(分钟)的函数解析式是 ;定义域是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com