
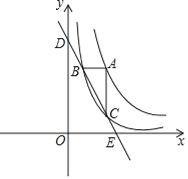
【题目】如图,点A在函数y=![]() (x>0)图象上,过点A作x轴和y轴的平行线分别交函数y=
(x>0)图象上,过点A作x轴和y轴的平行线分别交函数y=![]() 图象于点B,C,直线BC与坐标轴的交点为D,E.
图象于点B,C,直线BC与坐标轴的交点为D,E.
(1)当点C的横坐标为1时,求点B的坐标;
(2)试问:当点A在函数y=![]() (x>0)图象上运动时,△ABC的面积是否发生变化?若不变,请求出△ABC的面积,若变化,请说明理由.
(x>0)图象上运动时,△ABC的面积是否发生变化?若不变,请求出△ABC的面积,若变化,请说明理由.
(3)试说明:当点A在函数y=![]() (x>0)图象上运动时,线段BD与CE的长始终相等.
(x>0)图象上运动时,线段BD与CE的长始终相等.
【答案】(1)B点坐标为(![]() ,4);
,4);
(2)即△ABC的面积不发生变化,其面积为![]() ;
;
(3)证明见解析.
【解析】试题分析:(1)由条件可先求得A点坐标,从而可求得B点纵坐标,再代入y=![]() 可求得B点坐标;
可求得B点坐标;
(2)可设出A点坐标,从而可表示出C、B的坐标,则可表示出AB和AC的长,可求得△ABC的面积;
(3)可证明△ABC∽△EFC,利用(2)中,AB和AC的长可表示出EF,可得到BG=EF,从而可证明△DBG≌△CFE,可得到DB=CF.
解析:(1)∵点C在y=![]() 的图象上,且C点横坐标为1,
的图象上,且C点横坐标为1,
∴C(1,1),
∵AC∥y轴,AB∥x轴,
∴A点横坐标为1,
∵A点在函数y=![]() (x>0)图象上,
(x>0)图象上,
∴A(1,4),
∴B点纵坐标为4,
∵点B在y=![]() 的图象上,
的图象上,
∴B点坐标为(![]() ,4);
,4);
(2)设A(a,![]() ),则C(a,
),则C(a,![]() ),B(
),B(![]() ,
,![]() ),
),
∴AB=a﹣![]() =
=![]() a,AC=
a,AC=![]() ﹣
﹣![]() =
=![]() ,
,
∴S△ABC=![]() ABAC=
ABAC=![]() ,
,
即△ABC的面积不发生变化,其面积为![]() ;
;
(3)如图,设AB的延长线交y轴于点G,AC的延长线交x轴于点F,
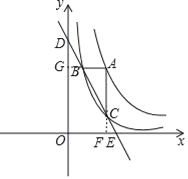
∵AB∥x轴,
∴△ABC∽△EFC,
∴![]() ,即
,即![]() ,
,
∴EF=![]() a,
a,
由(2)可知BG=![]() a,
a,
∴BG=EF,
∵AE∥y轴,∴∠BDG=∠FCE,
在△DBG和△CFE中
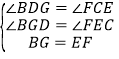
∴△DBG≌△CEF(AAS),
∴BD=EF.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】同时抛掷A,B两个均匀的小立方体(每个面上分别标有数字1,2,3,4,5,6),设两立方体朝上的数字分别为x,y,并以此确定点P(x,y),那么点P落在直线y=-2x+9上的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一块直角三角形木板,它的一条直角边AB长1.5m,面积为1.5m2.甲、乙两位木匠分别按图①、②把它加工成一个正方形桌面.请说明哪个正方形面积较大(加工损耗不计).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 至
至![]() ,点
,点![]() 的对应点分别是
的对应点分别是![]() ,连接
,连接![]() 线段
线段![]() 与线段
与线段![]() 交于点M,连接
交于点M,连接![]() .
.
(1)如图1,求证:![]() ;
;
(2)如图1,求证:OM平分![]() ;
;
(3)如图2,若![]() ,求
,求![]() 的长.
的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一辆汽车和一辆摩托车分别从A,B两地去同一城市,l1 ,l2分别表示汽车、摩托车离A地的距离s(km)随时间t(h)变化的图象,则下列结论:①摩托车比汽车晚到1 h;②A,B两地的距离为20 km;③摩托车的速度为45 km/h,汽车的速度为60 km/h;④汽车出发1 h后与摩托车相遇,此时距离B地40 km;⑤相遇前摩托车的速度比汽车的速度快.其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两根长度为12米的绳子,一端系在旗杆上的同一位置A点,另一端分别固定在地面上的两个木桩B,C上(绳结处的误差忽略不计),现在只有一把卷尺,如何检验旗杆是否垂直于地面BC?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
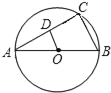
【题目】如图,已知AB为⊙O的直径,AC为弦,OD∥BC,交AC于D,BC=4cm.
(1)求证:AC⊥OD;
(2)求OD的长;
(3)若2sinA﹣1=0,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
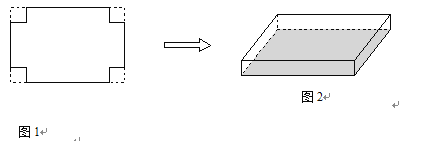
【题目】(本题满分8分)一张长为30cm,宽20cm的矩形纸片,如图1所示,将这张纸片的四个角各剪去一个边长相同的正方形后,把剩余部分折成一个无盖的长方体纸盒,如图1所示,如果折成的长方体纸盒的底面积为264cm2,求剪掉的正方形纸片的边长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com