
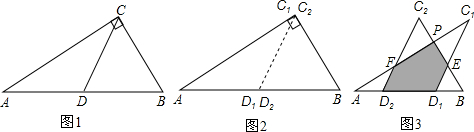
���� ��1������AD1=BD2�Ϳ���֤��AD2=BD1�����ݵȽǶԵȱ�֤��AD2=D2F��D1E=D1B���ɣ�
��2�����ڡ�AC1D1���BC2D2�ص�����Ϊ������ͼ�Σ����Խ������ת��ΪS��BC2D2-S��BED1-S��FC2P������������ε�������ɣ�
��3���ȼ������x��ֵʹ��y=$\frac{3}{8}$S��ABC���������ABC�������Ȼ����ݣ�2������y=-$\frac{18}{25}$x2+$\frac{24}{5}$x��0��x��5������������ϵ��ͨ�������б�ʽ���ж��Ƿ���������xֵ���ڣ�
��� �⣺��1��D1E=D2F���������£�
��C1D1��C2D2��
���C1=��AFD2��
�֡ߡ�ACB=90�㣬CD��б���ϵ����ߣ�
��DC=DA=DB����C1D1=C2D2=BD2=AD1
���C1=��A��
���AFD2=��A
��AD2=D2F��
ͬ����BD1=D1E��
�֡�AD1=BD2��
��AD2=BD1��
��D1E=D2F��
��2������Rt��ABC��AC=8��BC=6��
���ɹ��ɶ�������AB=10��
��AD1=BD2=C1D1=C2D2=5
�֡�D2D1=x��
��D1E=BD1=D2F=AD2=5-x��
��C2F=C1E=x
�ڡ�BC2D2�У�C2��BD2�ľ�����ǡ�ABC��AB���ϵĸߣ�Ϊ $\frac{24}{5}$��
���BED1��BD1���ϵĸ�Ϊh��
��̽�����á�BC2D2�ס�BED1��
��$\frac{h}{\frac{24}{5}}$=$\frac{5-x}{5}$��
��h=$\frac{24��5-x��}{25}$��S��BED1=$\frac{1}{2}$��BD1��h=$\frac{12}{25}$��5-x��2
�֡ߡ�C1+��C2=90�㣬
���FPC2=90�ȣ�
�֡ߡ�C2=��B��sinB=$\frac{4}{5}$��cosB=$\frac{3}{5}$��
��PC2=$\frac{3}{5}$x��PF=$\frac{4}{5}$x��S��FC2P=$\frac{1}{2}$PC2��PF=$\frac{6}{25}$x2
��y=S��BC2D2-S��BED1-S��FC2P=$\frac{1}{2}$S��ABC-$\frac{12}{25}$��5-x��2-$\frac{6}{25}$x2
��y=-$\frac{18}{25}$x2+$\frac{24}{5}$x��0��x��5����
��3�������ڣ�
��y=$\frac{3}{8}$S��ABCʱ����-$\frac{18}{25}$x2+$\frac{24}{5}$x=9��
������6x2-40x+75=0��
�ߡ�=1600-4��6��75=-200��0��
��÷����⣬�����ڣ�2���еĽ��۲�����������x��ʹ���ظ������������ԭ��ABCֽƬ�����$\frac{3}{8}$��
���� �����ۺ���ǿ������ͼ�ε�ƽ�ơ����κ�������ʽ��ȷ���Լ��ۺ����⡢�������⡢�������������������ȫ�森ͬʱ������һ�����������⣬�����Ƕ�̬���⣬��1С�ⲻ�ѽ������2С���һ���ѵ����������Ӱ���ֵ������Ҫע������������岹�η���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
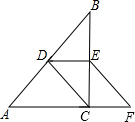 ��Rt��ABC�У���ACB=90�㣬D��E�ֱ�Ϊ��AB��BC���е㣬��F�ڱ�AC���ӳ����ϣ���FEC=��B����֤���ı���CDEF��ƽ���ı��Σ�
��Rt��ABC�У���ACB=90�㣬D��E�ֱ�Ϊ��AB��BC���е㣬��F�ڱ�AC���ӳ����ϣ���FEC=��B����֤���ı���CDEF��ƽ���ı��Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
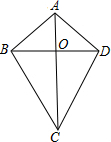 ��ͼ���ı���ABCD�У�AB=AD��CB=CD����Ƹ��ı���Ϊ�����Ρ������ӶԽ���AC��BD�����ڵ�O��
��ͼ���ı���ABCD�У�AB=AD��CB=CD����Ƹ��ı���Ϊ�����Ρ������ӶԽ���AC��BD�����ڵ�O���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
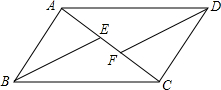 ��֪?ABCD�У�AC�ǶԽ��ߣ�BEƽ�֡�ABC��AC�ڵ�E��DFƽ�֡�ADC��AC�ڵ�F����֤��AE=CF��
��֪?ABCD�У�AC�ǶԽ��ߣ�BEƽ�֡�ABC��AC�ڵ�E��DFƽ�֡�ADC��AC�ڵ�F����֤��AE=CF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
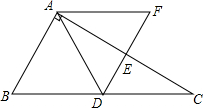 ��ͼ��Rt��ABC�У���BAC=90�㣬��C=30�㣮��D��E�ֱ��DZ�BC��AC���е㣬DE��������BC��ƽ����AF���ڵ�F��
��ͼ��Rt��ABC�У���BAC=90�㣬��C=30�㣮��D��E�ֱ��DZ�BC��AC���е㣬DE��������BC��ƽ����AF���ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com