
【题目】图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点.点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD、AN.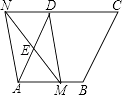
(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为时,四边形AMDN是矩形;
②当AM的值为时,四边形AMDN是菱形.
【答案】
(1)
证明:∵四边形ABCD是菱形,
∴ND∥AM,
∴∠NDE=∠MAE,∠DNE=∠AME,
又∵点E是AD边的中点,
∴DE=AE,
∴△NDE≌△MAE,
∴ND=MA,
∴四边形AMDN是平行四边形
(2)1;2
【解析】(2)解:①当AM的值为1时,四边形AMDN是矩形.理由如下:
∵四边形ABCD是菱形,
∴AB=AD=2.
∵AM= ![]() AD=1,
AD=1,
∴∠ADM=30°
∵∠DAM=60°,
∴∠AMD=90°,
∴平行四边形AMDN是矩形;
故答案为:1;
②当AM的值为2时,四边形AMDN是菱形.理由如下:
∵AM=2,
∴AM=AD=2,
∴△AMD是等边三角形,
∴AM=DM,
∴平行四边形AMDN是菱形,
故答案为:2.
(1)利用菱形的性质和已知条件可证明四边形AMDN的对边平行且相等即可;(2)①有(1)可知四边形AMDN是平行四边形,利用有一个角为直角的平行四边形为矩形即∠DMA=90°,所以AM= ![]() AD=1时即可;②当平行四边形AMND的邻边AM=DM时,四边形为菱形,利用已知条件再证明三角形AMD是等边三角形即可.
AD=1时即可;②当平行四边形AMND的邻边AM=DM时,四边形为菱形,利用已知条件再证明三角形AMD是等边三角形即可.


科目:初中数学 来源: 题型:
【题目】如图,某港口P位于东西方向的海岸线上“远航”号、“海天”号轮船同时离开港口,各自沿同定方向航行,“远航”号每小时航行16n mile,“海天”号每小时航行12n mile,它们离开港口一个半小时后分别位于点Q,R处,且相距30n mile 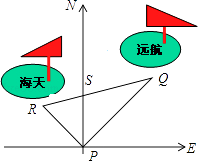
(1)求PQ,PR的长度;
(2)如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC=6,BD=8,点E、F分别是边AB、BC的中点,点P在AC上运动,在运动过程中,存在PE+PF的最小值,则这个最小值是 . 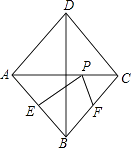
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一次,小明坐着轮船由A点出发沿正东方向AN航行,在A点望湖中小岛M,测得∠MAN=30°,航行100米到达B点时,测得∠MBN=45°,你能算出A点与湖中小岛M的距离吗? 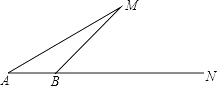
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一服装批发店出售某品牌童装,每件进价120元,批发价200元,多买优惠;凡是一次买10件以上的,每多买一件,所买的全部服装每件就降低1元,但是最低价为为每件160元,
(1)求一次至少买多少件,才能以最低价购买?
(2)写出服装店一次销售x件时,获利润y(元)与x(件)之间的函数关系式,并写出自变量x的取值范围;
(3)一天,甲批发了46件,乙批发了50件,店主却发现卖46件赚的钱反而比卖50件赚的钱多,你能用数学知识解释这一现象吗?为了不出现这种现象,在其他优惠条件不变的情况下,店家应把最低价每件160元至少提高到多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y= ![]() 的图象如图所示,以下结论: ①常数m<﹣1;
的图象如图所示,以下结论: ①常数m<﹣1;
②在每个象限内,y随x的增大而增大;
③若A(﹣1,h),B(2,k)在图象上,则h<k;
④若P(x,y)在图象上,则P′(﹣x,﹣y)也在图象上.
其中正确的是( )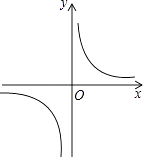
A.①②
B.②③
C.③④
D.①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com