
����Ŀ��һ��װ���������ijƷ��ͯװ��ÿ������120Ԫ��������200Ԫ�������Żݣ�����һ����10�����ϵģ�ÿ����һ���������ȫ����װÿ���ͽ���1Ԫ��������ͼ�ΪΪÿ��160Ԫ��
��1����һ����������ټ�����������ͼ۹���
��2��д����װ��һ������x��ʱ��������y��Ԫ����x������֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��3��һ�죬��������46������������50��������ȴ������46����Ǯ��������50����Ǯ�࣬��������ѧ֪ʶ������һ������Ϊ�˲��������������������Ż��������������£����Ӧ����ͼ�ÿ��160Ԫ������ߵ����٣�
���𰸡���1��һ��������50������������ͼ۹���2��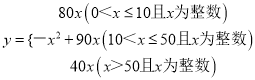 ����3�����Ӧ����ͼ�ÿ��160Ԫ������ߵ�165Ԫ��
����3�����Ӧ����ͼ�ÿ��160Ԫ������ߵ�165Ԫ��
�������������������1����һ��������x������ÿ���ļ۸�Ϊ[200-��x-10��]Ԫ�����ݽ��ۺ�ļ۸�Ϊ160Ԫ�������������⼴�ɣ�
��2������������=����������ÿ֧������������ʽ���ɣ�
��3�����ݣ�2���Ľ�����Ϊ����ʽ�����ݶ���ʽ�����ʾͿ���������ۣ�
���������
��1����һ��������x������������ͼ۹��������⣬��
200����x��10����1=160��
��ã�x��50��
��һ��������50������������ͼ۹���
��2����0��x��10ʱ��y��(200��120)x��80x
��10��x��50ʱ��y��[��200��120������x��10����1] ��x����x2+90x��
��x��50ʱ��y��(160��120)x��40x��
���ϣ�y��x�Ĺ�ϵʽΪ 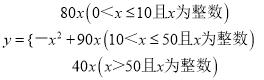
��3����y����x2+90x����(x��45)2+2025 ֪�Գ���x��45��
��45��x��50ʱ��y��x���������С���������ļ���Խ��ʱ������ԽС��
����������46����Ǯ����50���ӵ�Ǯ�������
��x��45ʱ������ۼ�Ϊ200����45��10����165��Ԫ����
��Ϊ�˲��������������������Ż��������������£����Ӧ����ͼ�ÿ��160Ԫ������ߵ�165Ԫ��


 ��ս100��Ԫ����Ծ�ϵ�д�
��ս100��Ԫ����Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������Ѿ���Խ�˺����������Ϊ�����й��˴���ǰ���ͷ���С���������������罻����Ҫ���壬2019���Ϧ�������ڼ䣬����8.23���˴��շ��ź��ͬ������7.12%���ÿ�ѧ��������ʾ8.23�������Ϊ��������
A.8.23��107B.8.23��108C.8.23��109D.0.83��109
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵���в���ȷ���У� �� �ٵ���ʽ��2��R2������Բ���ʣ���ϵ���ǩ�2��23x5��8�ε���ʽ��xy��1��һ�ζ���ʽ��
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ��������ABCD�У�AB=2����DAB=60�㣬��E��AD�ߵ��е㣮��M��AB����һ���㣨�����A�غϣ����ӳ�ME������CD�ڵ�N������MD��AN��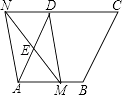
��1����֤���ı���AMDN��ƽ���ı��Σ�
��2����գ��ٵ�AM��ֵΪʱ���ı���AMDN�Ǿ��Σ�
�ڵ�AM��ֵΪʱ���ı���AMDN�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��ͷ����ֱ����ԼΪ 0.000 071 8 �ף�����0.000 071 8���ÿ�ѧ��������ʾ��ȷ���� ( )
A.��7.18��10 5B.��0.718��10 5
C.7.18��10 5D.0.718��10 5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
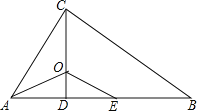
����Ŀ����ͼ����ABC�У���ACB=90����CD��AB�ڵ�D��AOƽ�֡�BAC����CD�ڵ�O��EΪAB��һ�㣬��AE=AC��
��1����֤����AOC�ա�A0E��
��2����֤��OE��BC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵��������������ǣ���
A.��һ������ֻ��һ��ֱ������ֱ֪��ƽ��
B.ͬλ�����
C.��ֱ��ͬһ��ֱ�ߵ�����ֱ����ƽ��
D.�Զ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���ABCD�У�AB��AC��AB=1��BC= ![]() ���Խ���AC��BD�ཻ�ڵ�O����ֱ��AC�Ƶ�O˳ʱ����ת���ֱ�BC��AD�ڵ�E��F��
���Խ���AC��BD�ཻ�ڵ�O����ֱ��AC�Ƶ�O˳ʱ����ת���ֱ�BC��AD�ڵ�E��F�� 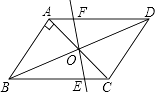
��1��֤��������AOF=90��ʱ���ı���ABEF��ƽ���ı��Σ�
��2����˵������ת�����У�AF��CE�ܱ�����ȣ�
��3������ת�����У��ı���BEDF������������������ܣ���˵�����ɣ�����ܣ�˵�����ɲ������ʱ��AOF������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com