
分析 由a和b互为相反数,得出a+b=0,a=-b,进一步利用平方差公式因式分解,代入求得a、b的数值,进一步代入求得结果即可.
解答 解:∵a和b互为相反数,
∴a+b=0,a=-b,
∵(a+3)2-(b+3)2=18,
∴(a+3+b+3)(a+3-b-3)=18,
∴6(a-b)=18,
即12a=18,
解得:a=$\frac{3}{2}$,
∴b=-$\frac{3}{2}$,
∴a2•b3=$\frac{9}{4}$×(-$\frac{27}{8}$)=-$\frac{243}{32}$.
故答案为:-$\frac{243}{32}$.
点评 此题考查因式分解的实际运用,相反数的意义,掌握平方差公式因式分解是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
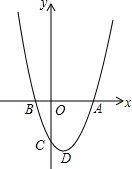 如图,已知抛物线y=ax2-2ax-b(a>0)与x轴的一个交点为B(-1,0),与y轴的负半轴交于点C,顶点为D.
如图,已知抛物线y=ax2-2ax-b(a>0)与x轴的一个交点为B(-1,0),与y轴的负半轴交于点C,顶点为D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com