Question

10．已知△ABC中，∠ABC=∠ACB，D为射线CB上一点（不与C、B重合），点E为射线CA上一点，∠ADE=∠AED．设∠BAD=α，∠CDE=β．
（1）如图（1），
①若∠BAC=40°，∠DAE=30°，则α=10°，β=5°．
②写出α与β的数量关系，并说明理由；
（2）如图（2），当D点在BC边上，E点在CA的延长线上时，其它条件不变，写出α与β的数量关系，并说明理由．
（3）如图（3），D在CB的延长线上，根据已知补全图形，并直接写出α与β的关系式$β=\frac{180°-α}{2}$．

Answer 1

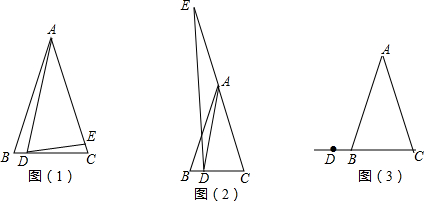
分析 （1）①根据等腰三角形的性质，利用三角形内角和定理和三角形外角的性质，利用等量代换即可求解；
②根据等腰三角形的性质，利用三角形内角和定理和三角形外角的性质，利用等量代换即可得到结论；
（2）设∠BAC=x°，∠DAE=y°，则∠CAD=180°-y°，根据三角形的内角和和外角的性质得到α=x°-（180°-y°）=x°-180°+y°，由三角形的内角和得到$∠C=\frac{180°-x°}{2}$$∠AED=\frac{180°-y°}{2}$，通过整理化简结论得到结论．
（3）方法同（2）．

解答 解：（1）①α=10°，β=5°；
故答案为：10°，5°；
②α=2β，
设∠BAC=x°，∠DAE=y°，则α=x°-y°
∵∠ABC=∠ACB
∴$∠C=\frac{180°-x°}{2}$
∵∠ADE=∠AED
∴$∠AED=\frac{180°-y°}{2}$
∴$β=\frac{180°-y°}{2}-\frac{180°-x°}{2}=\frac{x°-y°}{2}$
∴α=2β；

（2）$β=\frac{180°+α}{2}$，
设∠BAC=x°，∠DAE=y°，则∠CAD=180°-y°
∴α=x°-（180°-y°）=x°-180°+y°
∵∠ABC=∠ACB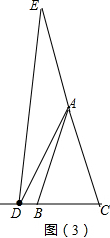
∴$∠C=\frac{180°-x°}{2}$
∵∠ADE=∠AED
∴$∠AED=\frac{180°-y°}{2}$
∴$β=180°-\frac{180°-y°}{2}-\frac{180°-x°}{2}=\frac{x°+y°}{2}$
∴$β=\frac{180°+α}{2}$；

（3）如图，$β=\frac{180°-α}{2}$，
设∠BAC=x°，∠DAE=y°，则∠CAD=180°-y°
∴α=180°-y°-x°=180°-y°-x°，
∵∠ABC=∠ACB
∴$∠C=\frac{180°-x°}{2}$
∵∠ADE=∠AED
∴$∠AED=\frac{180°-y°}{2}$，∴
∴$β=180°-\frac{180°-y°}{2}-\frac{180°-x°}{2}=\frac{x°+y°}{2}$
∴$β=\frac{180°-α}{2}$．
故答案为：$β=\frac{180°-α}{2}$．

点评 本题考查了三角形的内角和与三角形外角的性质，关键是结合图形灵活利用这两个性质定理列出角的关系进行推理．