
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x>0)的图象交于A(m,6),B(3,n)两点.
(x>0)的图象交于A(m,6),B(3,n)两点.
(1) 求一次函数的表达式;
(2) 根据图象写出kx+b-![]() <0的x的取值范围.
<0的x的取值范围.
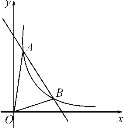
【答案】(1) 一次函数的解析式为y=-2x+8;(2) 0<x<1或x>3
【解析】
(1)先把A、B点坐标代入y=![]() ,求出m、n的值;然后将其分别代入一次函数解析式,列出关于系数k、b的方程组,通过解方程组求得它们的值即可;
,求出m、n的值;然后将其分别代入一次函数解析式,列出关于系数k、b的方程组,通过解方程组求得它们的值即可;
(2)根据该不等式的解集即为直线在双曲线下方时x的范围即可写出答案;
解:(1)∵点A(m,6),B(3,n)两点在反比例函数![]() (x>0)的图象上,
(x>0)的图象上,
∴6m=3n=6,
∴m=1,n=2,
∴A(1,6),B(3,2).
又∵点A(m,6),B(3,n)两点在一次函数y=kx+b的图象上,
∴![]()
解得![]()
则该一次函数的解析式为:y=2x+8;
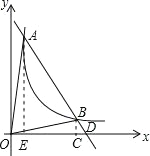
(2)根据图象可知使![]() 成立的x的取值范围是0<x<1或x>3;
成立的x的取值范围是0<x<1或x>3;


科目:初中数学 来源: 题型:
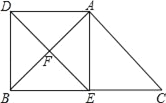
【题目】如图,E、F分别为△ABC的边BC、CA的中点,延长EF到D,使得DF=EF,连接DA、DB、AE.
(1)求证:四边形ACED是平行四边形;
(2)若AB=AC,试说明四边形AEBD是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“金源”食品加工厂需要一批食品包装盒,供应这种包装盒有两种方案可供选择:
方案一:从包装盒加工厂直接购买,购买所需的费用![]() (元)与包装盒个数
(元)与包装盒个数![]() (个)满足图中的射线
(个)满足图中的射线![]() 所示的函数关系;
所示的函数关系;
方案二:租赁机器自己加工,所需费用![]() (元)(包括租赁机器的费用和生产包装盒的费用)与包装盒个数
(元)(包括租赁机器的费用和生产包装盒的费用)与包装盒个数![]() (个)满足图中射线
(个)满足图中射线![]() 所示的函数关系.
所示的函数关系.
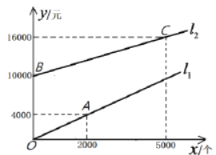
根据图象解答下列问题:
(1)点![]() 的坐标是_____________,方案一中每个包装盒的价格是___________元,射线
的坐标是_____________,方案一中每个包装盒的价格是___________元,射线![]() 所表示的函数关系式是_____________.
所表示的函数关系式是_____________.
(2)求出方案二中的![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)你认为选择哪种方案更省钱?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
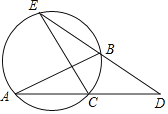
【题目】如图,A、B、C是⊙O上的点,D是弦AC的延长线一点,且BA=BD,DB的延长线交⊙O于E.
(1)求证:CD=CE;
(2)若C为AD的中点,求证:AB是⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
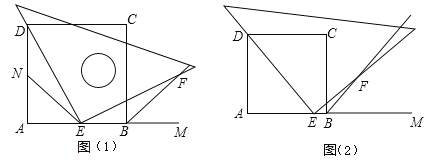
【题目】如图所示,四边形![]() 是正方形,
是正方形, ![]() 是
是![]() 延长线上一点.直角三角尺的一条直角边经过点
延长线上一点.直角三角尺的一条直角边经过点![]() ,且直角顶点
,且直角顶点![]() 在
在![]() 边上滑动(点
边上滑动(点![]() 不与点
不与点![]() 重合),另一直角边与
重合),另一直角边与![]() 的平分线
的平分线![]() 相交于点
相交于点![]() .
.
(1)求证: ![]() ;
;
(2)如图(1),当点![]() 在
在![]() 边的中点位置时,猜想
边的中点位置时,猜想![]() 与
与![]() 的数量关系,并证明你的猜想;
的数量关系,并证明你的猜想;
(3)如图(2),当点![]() 在
在![]() 边(除两端点)上的任意位置时,猜想此时
边(除两端点)上的任意位置时,猜想此时![]() 与
与![]() 有怎样的数量关系,并证明你的猜想.
有怎样的数量关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
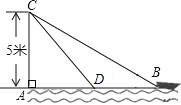
【题目】在杭州西湖风景游船处,如图,在离水面高度为5m的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13m,此人以0.5m/s的速度收绳.10s后船移动到点D的位置,问船向岸边移动了多少m?(假设绳子是直的,结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BE=CF,AB∥DE,添加下列哪个条件不能证明△ABC≌△DEF的是( )
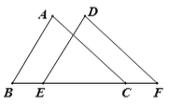
A. AB=DE B. ∠A=D C. AC=DF D. AC∥DF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,甲、乙两个容器内都装了一定数量的水,现将甲容器中的水匀速注入乙容器中.图2中的线段AB,CD分别表示容器中的水的深度h(厘米)与注入时间t(分钟)之间的函数图象.下列结论错误的是( )
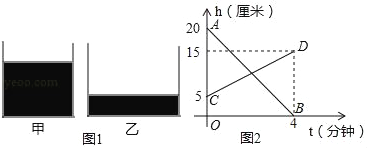
A. 注水前乙容器内水的高度是5厘米
B. 甲容器内的水4分钟全部注入乙容器
C. 注水2分钟时,甲、乙两个容器中的水的深度相等
D. 注水1分钟时,甲容器的水比乙容器的水深5厘米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2m+1)x+m2﹣2=0.
(1)若该方程有两个实数根,求m的最小整数值;
(2)若方程的两个实数根为x1,x2,且(x1﹣x2)2+m2=21,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com