
【题目】如图,菱形ABCD的边长为2cm,∠DAB=60°.点P从A点出发,以 ![]() cm/s的速度,沿AC向C作匀速运动;与此同时,点Q也从A点出发,以1cm/s的速度,沿射线AB作匀速运动.当P运动到C点时,P、Q都停止运动,设点P运动的时间为ts.
cm/s的速度,沿AC向C作匀速运动;与此同时,点Q也从A点出发,以1cm/s的速度,沿射线AB作匀速运动.当P运动到C点时,P、Q都停止运动,设点P运动的时间为ts. 
(1)点P由A点运动到C点需要秒;
(2)当P异于A、C时,请说明PQ∥BC;
(3)以P为圆心、PQ长为半径作圆,请问:在运动过程中,⊙P与边BC有2个公共点时t的取值范围?
【答案】
(1)2
(2)证明:连接BD交AC于点O.
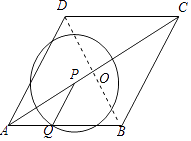
∵四边形ABCD是菱形,且边长为2cm,∠DAB=60°,
∴AB=BC=2,∠BAC= ![]() ∠BAD=30°,
∠BAD=30°,
∵AC⊥BD,OA= ![]() AC=
AC= ![]() ,
,
∴AC=2 ![]() ,∵AB=2,AP=
,∵AB=2,AP= ![]() t,AQ=t,
t,AQ=t,
∴ ![]() =
= ![]() .即
.即 ![]() =
= ![]() ,又∵∠PAQ=∠CAB,
,又∵∠PAQ=∠CAB,
∴△PAQ≌△CAB,
∴∠APQ=∠ACB,
∴PQ∥BC.
(3)解:当⊙P与边BC 相切与点M时,连接PM,则PM⊥BC,

在Rt△CPM中,
∵∠PCM=30°,
∴PM= ![]() PC=
PC= ![]() ﹣
﹣ ![]() t,又PM=PQ=AQ=t,
t,又PM=PQ=AQ=t,
即 ![]() ﹣
﹣ ![]() t=t,
t=t,
∴t=4 ![]() ﹣6,
﹣6,
当⊙P过点B时,PQ=PB,
∵∠PQB=∠PAQ+∠APQ=60°,
∴△PQB为等边三角形,
∴QB=PQ=AQ=t,
∴t=1.
综上,若使⊙P与边BC有2个公共点,则4 ![]() ﹣6<t≤1.
﹣6<t≤1.
【解析】解:(1)由题意AC= ![]() , ∴t=
, ∴t= ![]() =2s,
=2s,
所以答案是2.


科目:初中数学 来源: 题型:
【题目】在△ABC 中,边 AC,BC 的垂直平分线的交点 O 落在边 AB 上,则△ABC 的形状是( )
A. 钝角三角形 B. 直角三角形 C. 锐角三角形 D. 任意三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,己知数轴上点A表示的数为8,B是数轴上一点,且AB=22.动点P从点A出发,以每秒4个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)写出数轴上点B表示的数____,点P表示的数____(用含t的代数式表示);
(2)若动点Q从点B出发,以每秒2个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,问点P运动多少秒时追上点Q?(列一元一次方程解应用题)
(3)若动点Q从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,若点P、Q同时出发,问 秒时P、Q之间的距离恰好等于2(直接写出答案)
(4)思考在点P的运动过程中,若M为AP的中点,N为PB的中点.线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了推进球类运动的普及,成立了多个球类运动社团,为此,学生会采取抽样调查的方法,从足球、乒乓球、篮球、排球四个项目调查了若干名学生的兴趣爱好(要求每位同学只能选择其中一种自己喜欢的球类运动),并将调查结果绘制成了如下条形统计图和扇形统计图(不完整).请你根据图中提供的信息,解答下列问题: 
(1)求扇形统计图中,“乒乓球”所对应的扇形的圆心角为度;
(2)请将条形统计图和扇形统计图补充完整;
(3)若该学校共有学生1600人,根据以上数据分析,试估计选择排球运动的同学约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知等边△ABC的边长为a,P是△ABC内一点,PD∥AB,PE∥BC,PF∥AC,点D、E、F分别在BC、AC、AB上,猜想:PD+PE+PF等于多少,并证明你的猜想.
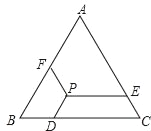
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中央电视台的“中国诗词大赛”节目文化品位高,内容丰富,某校初二年级模拟开展“中国诗词大赛”比赛,对全年级同学成绩进行统计后分为“优秀”、“良好”、“一般”、“较差”四个等级,并根据成绩绘制成如下两幅不完整的统计图,请结合统计图中的信息,回答下列问题: 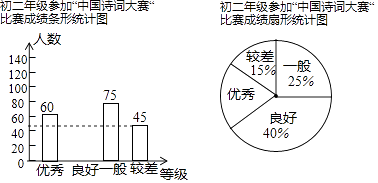
(1)扇形统计图中“优秀”所对应的扇形的圆心角为度,并将条形统计图补充完整 .
(2)此次比赛有四名同学活动满分,分别是甲、乙、丙、丁,现从这四名同学中挑选两名同学参加学校举行的“中国诗词大赛”比赛,请用列表法或画树状图法,求出选中的两名同学恰好是甲、丁的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
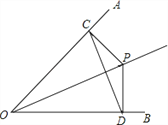
【题目】如图,已知P点是∠AOB平分线上一点,PC⊥OA,PD⊥OB,垂足为C、D.
(1)求证:∠PCD=∠PDC;
(2)求证:OP是线段CD的垂直平分线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com