
【题目】如图所示,已知等边△ABC的边长为a,P是△ABC内一点,PD∥AB,PE∥BC,PF∥AC,点D、E、F分别在BC、AC、AB上,猜想:PD+PE+PF等于多少,并证明你的猜想.
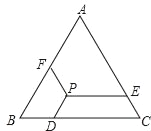
【答案】PD+PE+PF=a.理由见解析.
【解析】
延长EP交AB于G,延长FP交BC于H,然后证明△PFG和△PDH是等边三角形,根据等边三角形的性质求出PF=PG,PD=DH,再证明四边形BDPG和四边形CEPH是平行四边形,根据平行四边形的对边相等可得PG=BD,PE=CH,从而求出PD+PE+PF=BC.
解:PD+PE+PF=a.理由如下:
如图,延长EP交AB于G,延长FP交BC于H,
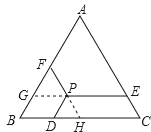
∵PE∥BC,PF∥AC,△ABC是等边三角形,
∴∠PGF=∠B=60°,∠PFG=∠A=60°,
∴△PFG是等边三角形,
同理可得△PDH是等边三角形,
∴PF=PG,PD=DH,
又∵PD∥AB,PE∥BC,
∴四边形BDPG是平行四边形,
∴PG=BD,
∴PD+PE+PF=DH+CH+BD=BC=a.


科目:初中数学 来源: 题型:
【题目】目前,步行已成为人们最喜爱的健身方法之一,通过手机可以计算行走的步数与相应的能量消耗.对比手机数据发现:小琼步行13500步与小刚步行9000步消耗的能量相同,若每消耗1千卡能量小琼行走的步数比小刚多15步,求小刚每消耗1千卡能量需要行走多少步?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:探究一次函数y=kx+k+2(k是不为0常数)图象的共性特点,探究过程:小明尝试把x=﹣1代入时,发现可以消去k,竟然求出了y=2.老师问:结合一次函数图象,这说明了什么?小组讨论得出:无论k取何值,一次函数y=kx+k+2的图象一定经过定点(﹣1,2),老师:如果一次函数的图象是经过某一个定点的直线,那么我们把像这样的一次函数的图象定义为“点旋转直线”.已知一次函数y=(k+3)x+(k﹣1)的图象是“点选直线”
(1)一次函数y=(k+3)x+(k﹣1)的图象经过的顶点P的坐标是 .
(2)已知一次函数y=(k+3)x+(k﹣1)的图象与x轴、y轴分别相交于点A、B
①若△OBP的面积为3,求k值;
②若△AOB的面积为1,求k值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E、F分别是AB、DC边上的点,且AE=CF, 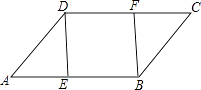
(1)求证:△ADE≌△CBF.
(2)若∠DEB=90°,求证:四边形DEBF是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为2cm,∠DAB=60°.点P从A点出发,以 ![]() cm/s的速度,沿AC向C作匀速运动;与此同时,点Q也从A点出发,以1cm/s的速度,沿射线AB作匀速运动.当P运动到C点时,P、Q都停止运动,设点P运动的时间为ts.
cm/s的速度,沿AC向C作匀速运动;与此同时,点Q也从A点出发,以1cm/s的速度,沿射线AB作匀速运动.当P运动到C点时,P、Q都停止运动,设点P运动的时间为ts. 
(1)点P由A点运动到C点需要秒;
(2)当P异于A、C时,请说明PQ∥BC;
(3)以P为圆心、PQ长为半径作圆,请问:在运动过程中,⊙P与边BC有2个公共点时t的取值范围?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A、B两个村庄的坐标分别是(2,1)和(6,3),一辆汽车从原点O出发,沿x轴向右行驶.
(1)当汽车行驶到点M(___________)时离A村最近;
(2)当汽车行驶到点N(____________)时离B村最近;
(3)当汽车行驶到点P(___________)时离A、B两村一样近.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y= ![]() (k≠0)的图象交于A、B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=4
(k≠0)的图象交于A、B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=4 ![]() ,cos∠ACH=
,cos∠ACH= ![]() ,点B的坐标为(4,n)
,点B的坐标为(4,n) 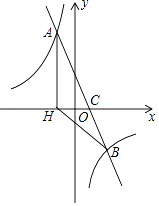
(1)求该反比例函数和一次函数的解析式;
(2)求△BCH的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算(直接写出结果):
(1)﹣2+5
(2)﹣17+(﹣3)
(3)(﹣10)﹣(-6)
(4)(﹣1![]() )×(﹣12)
)×(﹣12)
(5)﹣2×(﹣3)2
(6)﹣1![]() ÷(﹣5)
÷(﹣5)
(7)﹣1200+(﹣1)200
(8)﹣0.125×(﹣2)3
(9)|﹣![]() |
|
(10)(-![]() )3
)3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,张老师出示了问题:如图1,AC,BD是四边形ABCD的对角线,若∠ACB=∠ACD=∠ABD=∠ADB=60°,则线段BC,CD,AC三者之间有何等量关系?
经过思考,小明展示了一种正确的思路:如图2,延长CB到E,使BE=CD,连接AE,证得△ABE≌△ADC,从而容易证明△ACE是等边三角形,故AC=CE,所以AC=BC+CD.
小亮展示了另一种正确的思路:如图3,将△ABC绕着点A逆时针旋转60°,使AB与AD重合,从而容易证明△ACF是等边三角形,故AC=CF,所以AC=BC+CD.
在此基础上,同学们作了进一步的研究: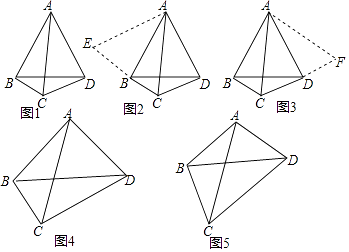
(1)小颖提出:如图4,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=45°”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小颖提出的问题,请你写出结论,并给出证明.
(2)小华提出:如图5,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=α”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小华提出的问题,请你写出结论,不用证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com