
【题目】数学课上,张老师出示了问题:如图1,AC,BD是四边形ABCD的对角线,若∠ACB=∠ACD=∠ABD=∠ADB=60°,则线段BC,CD,AC三者之间有何等量关系?
经过思考,小明展示了一种正确的思路:如图2,延长CB到E,使BE=CD,连接AE,证得△ABE≌△ADC,从而容易证明△ACE是等边三角形,故AC=CE,所以AC=BC+CD.
小亮展示了另一种正确的思路:如图3,将△ABC绕着点A逆时针旋转60°,使AB与AD重合,从而容易证明△ACF是等边三角形,故AC=CF,所以AC=BC+CD.
在此基础上,同学们作了进一步的研究: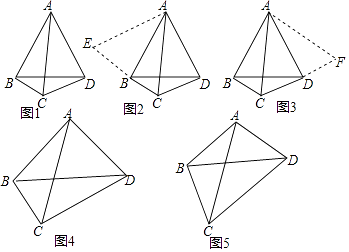
(1)小颖提出:如图4,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=45°”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小颖提出的问题,请你写出结论,并给出证明.
(2)小华提出:如图5,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=α”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小华提出的问题,请你写出结论,不用证明.
【答案】
(1)
解:BC+CD= ![]() AC;
AC;
理由:如图1,
延长CD至E,使DE=BC,
∵∠ABD=∠ADB=45°,
∴AB=AD,∠BAD=180°﹣∠ABD﹣∠ADB=90°,
∵∠ACB=∠ACD=45°,
∴∠ACB+∠ACD=45°,
∴∠BAD+∠BCD=180°,
∴∠ABC+∠ADC=180°,
∵∠ADC+∠ADE=180°,
∴∠ABC=∠ADE,
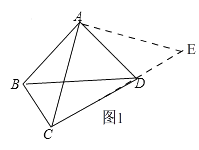
在△ABC和△ADE中, 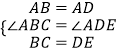 ,
,
∴△ABC≌△ADE(SAS),
∴∠ACB=∠AED=45°,AC=AE,
∴△ACE是等腰直角三角形,
∴CE= ![]() AC,
AC,
∵CE=CE+DE=CD+BC,
∴BC+CD= ![]() AC
AC
(2)
解:BC+CD=2ACcosα.理由:如图2,
延长CD至E,使DE=BC,
∵∠ABD=∠ADB=α,
∴AB=AD,∠BAD=180°﹣∠ABD﹣∠ADB=180°﹣2α,
∵∠ACB=∠ACD=α,
∴∠ACB+∠ACD=2α,
∴∠BAD+∠BCD=180°,
∴∠ABC+∠ADC=180°,
∵∠ADC+∠ADE=180°,
∴∠ABC=∠ADE,
在△ABC和△ADE中, 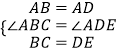 ,
,
∴△ABC≌△ADE(SAS),
∴∠ACB=∠AED=α,AC=AE,
∴∠AEC=α,
过点A作AF⊥CE于F,
∴CE=2CF,在Rt△ACF中,∠ACD=α,CF=ACcos∠ACD=ACcosα,
∴CE=2CF=2ACcosα,
∵CE=CD+DE=CD+BC,
∴BC+CD=2ACcosα

【解析】(1)先判断出∠ADE=∠ABC,即可得出△ACE是等腰三角形,再得出∠AEC=45°,即可得出等腰直角三角形,即可;(判断∠ADE=∠ABC也可以先判断出点A,B,C,D四点共圆)(2)先判断出∠ADE=∠ABC,即可得出△ACE是等腰三角形,再用三角函数即可得出结论.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:
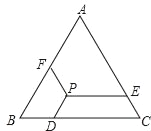
【题目】如图所示,已知等边△ABC的边长为a,P是△ABC内一点,PD∥AB,PE∥BC,PF∥AC,点D、E、F分别在BC、AC、AB上,猜想:PD+PE+PF等于多少,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O与Rt△ABC的直角边AC和斜边AB分别相切于点C、D,与边BC相交于点F,OA与CD相交于点E,连接FE并延长交AC边于点G. 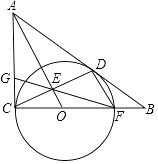
(1)求证:DF∥AO;
(2)若AC=6,AB=10,求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
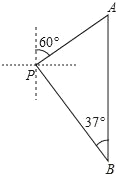
【题目】小亮一家到桃林口水库游玩.在岸边码头P处,小亮和爸爸租船到库区游玩,妈妈在岸边码头P处观看小亮与爸爸在水面划船,小船从P处出发,沿北偏东60°方向划行,划行速度是20米/分钟,划行10分钟后到A处,接着向正南方向划行一段时间到B处,在B处小亮观测到妈妈所在的P处在北偏西37°的方向上,这时小亮与妈妈相距多少米?(精确到1m,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
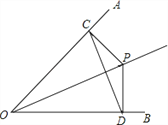
【题目】如图,已知P点是∠AOB平分线上一点,PC⊥OA,PD⊥OB,垂足为C、D.
(1)求证:∠PCD=∠PDC;
(2)求证:OP是线段CD的垂直平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF.下列条件使四边形BECF为菱形的是( ) 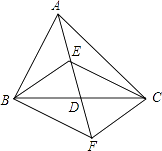
A.BE⊥CE
B.BF∥CE
C.BE=CF
D.AB=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园手机”现象越来越受到社会的关注.小丽在“统计实习”活动中随机调查了学校若干名学生家长对“中学生带手机到学校”现象的看法,统计整理并制作了如下的统计图: 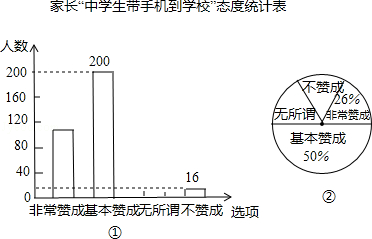
(1)求这次调查的家长总数及家长表示“无所谓”的人数,并补全图①;
(2)求图②中表示家长“无所谓”的圆心角的度数;
(3)从这次接受调查的家长中,随机抽查一个,恰好是“不赞成”态度的家长的概率是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A、B重合),BE⊥CD于E,交直线AC于F.
(1)点D在边AB上时,证明:AB=FA+BD;
(2)点D在AB的延长线或反向延长线上时,(1)中的结论是否成立?若不成立,请画出图形并直接写出正确结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D为直线BC上一动点(点D不与B、C重合)以AD为边作正方形ADEF,使∠DAF=∠BAC,连接CF.
(1)如图1,当点D在线段BC上时,求证:BD=CF;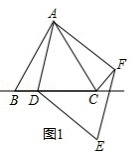
(2)如图2,当点D在线段BC的延长线上,且∠BAC=90°时.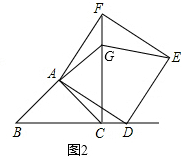
①问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
②延长BA交CF于点G,连接GE,若AB=2 ![]() ,CD=BC,请求出GE的长.
,CD=BC,请求出GE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com