
【题目】问题:探究一次函数y=kx+k+2(k是不为0常数)图象的共性特点,探究过程:小明尝试把x=﹣1代入时,发现可以消去k,竟然求出了y=2.老师问:结合一次函数图象,这说明了什么?小组讨论得出:无论k取何值,一次函数y=kx+k+2的图象一定经过定点(﹣1,2),老师:如果一次函数的图象是经过某一个定点的直线,那么我们把像这样的一次函数的图象定义为“点旋转直线”.已知一次函数y=(k+3)x+(k﹣1)的图象是“点选直线”
(1)一次函数y=(k+3)x+(k﹣1)的图象经过的顶点P的坐标是 .
(2)已知一次函数y=(k+3)x+(k﹣1)的图象与x轴、y轴分别相交于点A、B
①若△OBP的面积为3,求k值;
②若△AOB的面积为1,求k值.
【答案】
(1)(﹣1,﹣4)
(2)
∵一次函数y=(k+3)x+(k﹣1)的图象与x轴、y轴分别相交于点A、B
∴A( ![]() ,0),B(0,k﹣1).
,0),B(0,k﹣1).
①∵△OBP的面积为3,
∴ ![]() |k﹣1|=3,解得k=7或﹣5;
|k﹣1|=3,解得k=7或﹣5;
②∵△AOB的面积为1,
∴ ![]() ×|k﹣1|×|
×|k﹣1|×| ![]() |=1,解得k=5或﹣1.
|=1,解得k=5或﹣1.
【解析】解:(1)∵一次函数y=(k+3)x+(k﹣1)整理为y=k(x+1)+3x﹣1的形式,
∴令x+1=0,则x=﹣1,
∴y=﹣4,
∴P(﹣1,﹣4).
所以答案是:(﹣1,﹣4);
【考点精析】解答此题的关键在于理解一次函数的性质的相关知识,掌握一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2) 如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=![]() ,其中
,其中![]() 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系上,△ABC的顶点A和C分别在x轴、y轴的正半轴上,且AB∥y轴,点B(1,3),将△ABC以点B为旋转中心顺时针方向旋转90°得到△DBE,恰好有一反比例函数y= ![]() 图象恰好过点D,则k的值为( )
图象恰好过点D,则k的值为( ) 
A.6
B.﹣6
C.9
D.﹣9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某电脑公司有A型、B型、C型三种型号的电脑,其价格分别为A型每台6 000元,B型每台4 000元,C型每台2 500元,我市东坡中学计划将100 500元钱全部用于该电脑公司购进其中两种不同型号的电脑共36台,请你设计出几种不同的购买方案供该校选择,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,己知数轴上点A表示的数为8,B是数轴上一点,且AB=22.动点P从点A出发,以每秒4个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)写出数轴上点B表示的数____,点P表示的数____(用含t的代数式表示);
(2)若动点Q从点B出发,以每秒2个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,问点P运动多少秒时追上点Q?(列一元一次方程解应用题)
(3)若动点Q从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,若点P、Q同时出发,问 秒时P、Q之间的距离恰好等于2(直接写出答案)
(4)思考在点P的运动过程中,若M为AP的中点,N为PB的中点.线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
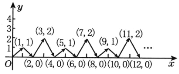
【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2)…按这样的运动规律,经过第2015次运动后,动点P的坐标是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了推进球类运动的普及,成立了多个球类运动社团,为此,学生会采取抽样调查的方法,从足球、乒乓球、篮球、排球四个项目调查了若干名学生的兴趣爱好(要求每位同学只能选择其中一种自己喜欢的球类运动),并将调查结果绘制成了如下条形统计图和扇形统计图(不完整).请你根据图中提供的信息,解答下列问题: 
(1)求扇形统计图中,“乒乓球”所对应的扇形的圆心角为度;
(2)请将条形统计图和扇形统计图补充完整;
(3)若该学校共有学生1600人,根据以上数据分析,试估计选择排球运动的同学约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
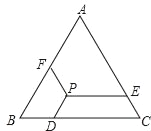
【题目】如图所示,已知等边△ABC的边长为a,P是△ABC内一点,PD∥AB,PE∥BC,PF∥AC,点D、E、F分别在BC、AC、AB上,猜想:PD+PE+PF等于多少,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O与Rt△ABC的直角边AC和斜边AB分别相切于点C、D,与边BC相交于点F,OA与CD相交于点E,连接FE并延长交AC边于点G. 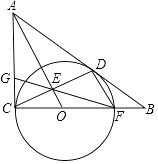
(1)求证:DF∥AO;
(2)若AC=6,AB=10,求CG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com