
����Ŀ��ijѧУΪ���ƽ������˶����ռ��������˶�������˶����ţ�Ϊ�ˣ�ѧ�����ȡ��������ķ�����������ƹ�������������ĸ���Ŀ������������ѧ������Ȥ���ã�Ҫ��ÿλͬѧֻ��ѡ������һ���Լ�ϲ���������˶������������������Ƴ�����������ͳ��ͼ������ͳ��ͼ�������������������ͼ���ṩ����Ϣ������������⣺ 
��1��������ͳ��ͼ�У���ƹ��������Ӧ�����ε�Բ�Ľ�Ϊ�ȣ�
��2���뽫����ͳ��ͼ������ͳ��ͼ����������
��3������ѧУ����ѧ��1600�ˣ������������ݷ������Թ���ѡ�������˶���ͬѧԼ�ж����ˣ�
���𰸡�
��1��144
��2���߱��ε����������Ϊ100��25%=400���ˣ���
��ƹ�����������400��40%=160���ˣ��������������400��100��160��40=100���ˣ���
������ռ�İٷֱ�Ϊ�� ![]() ��100%=25%��������ռ�İٷֱ�Ϊ��
��100%=25%��������ռ�İٷֱ�Ϊ�� ![]() ��100%=10%��
��100%=10%��
��ͼ��ʾ��
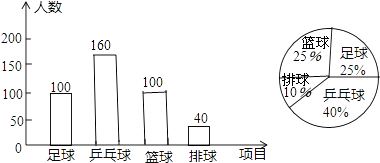
��3��1600��10%=160���ˣ���
������ѧУ����ѧ��1600�ˣ������������ݷ���������ѡ�������˶���ͬѧԼ��160�ˣ�
���������⣺��1��360���40%=144�㣬 ������ͳ��ͼ�У���ƹ��������Ӧ�����ε�Բ�Ľ�Ϊ144�㣬
���Դ��ǣ�144��
�����㾫����������Ŀ����֪��������������ͳ��ͼ������ͳ��ͼ�����֪ʶ���Եõ�����Ĵ𰸣���Ҫ����������ر�ʾ������������������ռ�İٷֱȣ����Dz�������ر�ʾ��ÿ����Ŀ�ľ�����Ŀ�Լ�����ı仯�����������ر�ʾ��ÿ����Ŀ�ľ�����Ŀ�����Dz�������ر�ʾ��������������������ռ�İٷֱ��Լ�����ı仯�����


 ��ҵ����ϵ�д�
��ҵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ƻ�Ͷ��14����Ԫʵʩ����ս�ԣ�Ϊ�˽���Զ���ս�ԵĹ�ע������Ѽ�����ɷò������Բɷ����������ͳ��ͼ����һ�������£�
��ע��� | Ƶ�� | Ƶ�� |
A���߶ȹ�ע | m | 0.1 |
B��һ���ע | 200 | 0.5 |
C������ע | 60 | n |
D����֪�� | 100 | 0.25 |
(1)�ɷ�������Ϊ__ __�ˣ�m��__ __��n��__ __��
(2)��ȫͳ��ͼ��
(3)������30 000�����и߶ȹ�ע����ս�Ե�����ԼΪ �ˣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʦ������ʦ������ʦ��Ů����Ҧ��ʦ��λ��ѧ��ʦ�����μ����ٳ�Ƭ�����ʦ�����ѡ��������ͨ����ǩ�����ϿνڴΣ���ǩʱŮʿ����
��1���ȳ�ȡ������ʦ��ϣ���ϵ�һ�ڿΣ�ȴƫƫ�鵽�ϵ�һ�ڿεĸ�������
��2��������ʦ�Ѿ��鵽�ϵ�һ�ڿε������£����ǩ����У�����ʦ��Ҧ��ʦ���Ͽεĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����⣺̽��һ�κ���y=kx+k+2��k�Dz�Ϊ0������ͼ��Ĺ����ص㣬̽�����̣�С������x=��1����ʱ�����ֿ�����ȥk����Ȼ�����y=2����ʦ�ʣ����һ�κ���ͼ����˵����ʲô��С�����۵ó�������kȡ��ֵ��һ�κ���y=kx+k+2��ͼ��һ���������㣨��1��2������ʦ�����һ�κ�����ͼ���Ǿ���ijһ�������ֱ�ߣ���ô���ǰ���������һ�κ�����ͼ����Ϊ������תֱ�ߡ�����֪һ�κ���y=��k+3��x+��k��1����ͼ���ǡ���ѡֱ�ߡ�
��1��һ�κ���y=��k+3��x+��k��1����ͼ���Ķ���P�������� ��
��2����֪һ�κ���y=��k+3��x+��k��1����ͼ����x�ᡢy��ֱ��ཻ�ڵ�A��B
������OBP�����Ϊ3����kֵ��
������AOB�����Ϊ1����kֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͬһƽ��ֱ������ϵ�У�����y=kx+k��y= ![]() ��k��0����ͼ������ǣ� ��
��k��0����ͼ������ǣ� ��
A.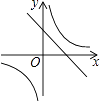
B.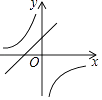
C.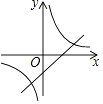
D.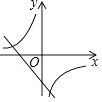
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�E��F�ֱ���AB��DC���ϵĵ㣬��AE=CF�� 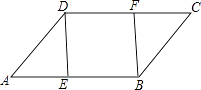
��1����֤����ADE�ա�CBF��
��2������DEB=90�㣬��֤���ı���DEBF�Ǿ��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ı߳�Ϊ2cm����DAB=60�㣮��P��A��������� ![]() cm/s���ٶȣ���AC��C�������˶������ͬʱ����QҲ��A���������1cm/s���ٶȣ�������AB�������˶�����P�˶���C��ʱ��P��Q��ֹͣ�˶������P�˶���ʱ��Ϊts��
cm/s���ٶȣ���AC��C�������˶������ͬʱ����QҲ��A���������1cm/s���ٶȣ�������AB�������˶�����P�˶���C��ʱ��P��Q��ֹͣ�˶������P�˶���ʱ��Ϊts�� 
��1����P��A���˶���C����Ҫ�룻
��2����P����A��Cʱ����˵��PQ��BC��
��3����PΪԲ�ġ�PQ��Ϊ�뾶��Բ�����ʣ����˶������У���P���BC��2��������ʱt��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=ax+b��a��0����ͼ���뷴��������y= ![]() ��k��0����ͼ����A��B���㣬��x�ύ�ڵ�C������A��AH��x���ڵ�H����O���߶�CH���е㣬AC=4
��k��0����ͼ����A��B���㣬��x�ύ�ڵ�C������A��AH��x���ڵ�H����O���߶�CH���е㣬AC=4 ![]() ��cos��ACH=
��cos��ACH= ![]() ����B��������4��n��
����B��������4��n�� 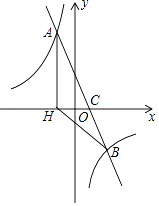
��1����÷�����������һ�κ����Ľ���ʽ��
��2�����BCH�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC �У�AB=AC=6cm����B=��C��BC=4cm���� D Ϊ AB���е㣮
��1������� P ���߶� BC ���� 1cm/s ���ٶ��ɵ� B ��� C �˶���ͬʱ���� Q ���߶� CA ���ɵ� C ��� A �˶���
������ Q ���˶��ٶ���� P ���˶��ٶ���ȣ����� 1 �����BPD ����CQP �Ƿ�ȫ�ȣ���˵�����ɣ�
������ Q ���˶��ٶ���� P ���˶��ٶȲ���ȣ����� Q ���˶��ٶ�Ϊ����ʱ���ܹ�ʹ��BPD ����CQP ȫ�ȣ�
��2������ Q �Ԣ��е��˶��ٶȴӵ� C �������� P ��ԭ�����˶��ٶȴӵ� B ͬʱ����������ʱ���ء�ABC �����˶����� �� P ��� Q ��һ���ڡ�ABC �� �������������ں�����ֱ��д���𰸣�������д������̣�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com