
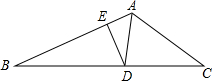
 如图,△ABC中,∠BAC=120°,AB=8,AC=6,AD平分∠BAC,交BC于点D,DE⊥AB于E,则DE=$\frac{12\sqrt{3}}{7}$.
如图,△ABC中,∠BAC=120°,AB=8,AC=6,AD平分∠BAC,交BC于点D,DE⊥AB于E,则DE=$\frac{12\sqrt{3}}{7}$. 分析 过B作BM⊥AD交AD的延长线于M,过C作CN⊥AD与N,根据已知条件得到∠BAD=∠CAD=60°,根据三角形的内角和得到∠ABM=∠ACN=30°,解直角三角形得到AM=$\frac{1}{2}$AB=4,AN=$\frac{1}{2}$AC=3,MB=$\frac{\sqrt{3}}{2}$AB=4$\sqrt{3}$,CN=$\frac{\sqrt{3}}{2}$AC=3$\sqrt{3}$,求得MN=1,根据相似三角形的性质得到$\frac{DM}{DN}=\frac{BM}{CN}=\frac{4}{3}$,求得DN=$\frac{3}{7}$,得到AD=$\frac{24}{7}$,然后根据直角三角形的性质即可得到结论.
解答 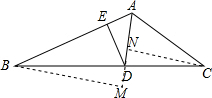 解:过B作BM⊥AD交AD的延长线于M,过C作CN⊥AD与N,
解:过B作BM⊥AD交AD的延长线于M,过C作CN⊥AD与N,
∵∠BAC=120°,AD平分∠BAC,
∴∠BAD=∠CAD=60°,
∴∠ABM=∠ACN=30°,
∵AB=8,AC=6,
∴AM=$\frac{1}{2}$AB=4,AN=$\frac{1}{2}$AC=3,MB=$\frac{\sqrt{3}}{2}$AB=4$\sqrt{3}$,CN=$\frac{\sqrt{3}}{2}$AC=3$\sqrt{3}$,
∴MN=1,
∵∠AMB=∠ANC=90°,∠BDM=∠CDN,
∴△BDM∽△CDN,
∴$\frac{DM}{DN}=\frac{BM}{CN}=\frac{4}{3}$,
∴DN=$\frac{3}{7}$,
∴AD=$\frac{24}{7}$,
∵DE⊥AB于E,
∴∠AED=90°,
∴∠ADE=30°,
∴DE=$\frac{\sqrt{3}}{2}$AD=$\frac{12\sqrt{3}}{7}$.
故答案为:$\frac{12\sqrt{3}}{7}$.
点评 本题考查了含30°角的直角三角形的性质,相似三角形的判定和性质,正确的作出辅助线构造相似三角形是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
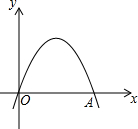 如图,已知抛物线的顶点在第一象限,顶点到x轴的距离为3,抛物线与x轴交于原点O(0,0)及点A,且OA=4.
如图,已知抛物线的顶点在第一象限,顶点到x轴的距离为3,抛物线与x轴交于原点O(0,0)及点A,且OA=4.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
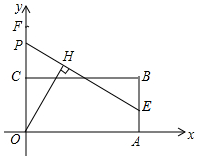 如图,矩形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(7,3),点E在边AB上,且AE=1,已知点P为y轴上一动点,连接EP,过点O作直线EP的垂线段,垂足为点H,在点P从点F(0,$\frac{25}{4}$)运动到原点O的过程中,点H的运动路径长为$\frac{5\sqrt{2}π}{4}$.
如图,矩形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(7,3),点E在边AB上,且AE=1,已知点P为y轴上一动点,连接EP,过点O作直线EP的垂线段,垂足为点H,在点P从点F(0,$\frac{25}{4}$)运动到原点O的过程中,点H的运动路径长为$\frac{5\sqrt{2}π}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
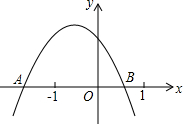 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,图象与x轴交于A(x1,0)B(x2,0)两点,点M(x0,y0)是图象上另一点,且x0>1.现有以下结论:①abc>0;②b<2a;③a+b+c>0;④a(x0-x1)(x0-x2)<0.
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,图象与x轴交于A(x1,0)B(x2,0)两点,点M(x0,y0)是图象上另一点,且x0>1.现有以下结论:①abc>0;②b<2a;③a+b+c>0;④a(x0-x1)(x0-x2)<0.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
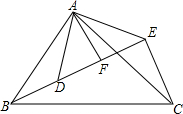 已知:如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,点B,D,E在同一直线上,AF⊥BE于点F,那么线段BE,CE,AF三者之间的数量关系是BE=CE+2AF.
已知:如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,点B,D,E在同一直线上,AF⊥BE于点F,那么线段BE,CE,AF三者之间的数量关系是BE=CE+2AF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com