
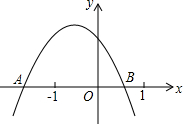
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,图象与x轴交于A(x1,0)B(x2,0)两点,点M(x0,y0)是图象上另一点,且x0>1.现有以下结论:①abc>0;②b<2a;③a+b+c>0;④a(x0-x1)(x0-x2)<0.
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,图象与x轴交于A(x1,0)B(x2,0)两点,点M(x0,y0)是图象上另一点,且x0>1.现有以下结论:①abc>0;②b<2a;③a+b+c>0;④a(x0-x1)(x0-x2)<0.分析 由抛物线的开口方向可确定a的符号,由抛物线的对称轴相对于y轴的位置可得a与b之间的符号关系,由抛物线与y轴的交点位置可确定c的符号;根据抛物线的对称轴与x=-1的大小关系可推出2a-b的符号;由于x=1时y=a+b+c,因而结合图象,可根据x=1时y的符号来确定a+b+c的符号,根据a、x0-x1、x0-x2的符号可确定a(x0-x1)(x0-x2)的符号.
解答 解:由抛物线的开口向下可得a<0,
由抛物线的对称轴在y轴的左边可得x=-$\frac{b}{2a}$<0,则a与b同号,因而b<0,
由抛物线与y轴的交点在y轴的正半轴上可得c>0,
∴abc>0,故①正确;
由抛物线的对称轴x=-$\frac{b}{2a}$>-1(a<0),可得-b<-2a,即b>2a,故②错误;
由图可知当x=1时y<0,即a+b+c<0,故③错误;
∵a<0,x0-x1>0,x0-x2>0,∴a(x0-x1)(x0-x2)<0,故④正确.
综上所述:①、④正确.
故答案为①、④.
点评 本题主要考查二次函数图象与系数的关系,其中a决定于抛物线的开口方向,b决定于抛物线的开口方向及抛物线的对称轴相对于y轴的位置,c决定于抛物线与y轴的交点位置,2a与b的大小决定于a的符号及-$\frac{b}{2a}$与-1的大小关系,运用数形结合的思想准确获取相关信息是解决本题的关键.


 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:初中数学 来源: 题型:解答题
| 购买苹果数 | 不超过30kg | 30kg以上但不超过50kg | 50kg以上 |
| 单价 | 3元 | 2.5元 | 2元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
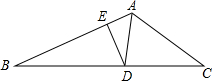 如图,△ABC中,∠BAC=120°,AB=8,AC=6,AD平分∠BAC,交BC于点D,DE⊥AB于E,则DE=$\frac{12\sqrt{3}}{7}$.
如图,△ABC中,∠BAC=120°,AB=8,AC=6,AD平分∠BAC,交BC于点D,DE⊥AB于E,则DE=$\frac{12\sqrt{3}}{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
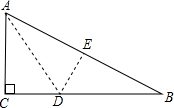 如图一直角三角形纸片,两直角边AC=3cm,BC=4cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
如图一直角三角形纸片,两直角边AC=3cm,BC=4cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )| A. | 2cm | B. | 3cm | C. | 1.5cm | D. | 4cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
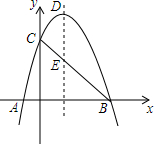 如图,抛物线y=-x2+2x+3与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.
如图,抛物线y=-x2+2x+3与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com