
分析 (1)根据题意方程有两个实数根,则△≥0且k-1≠0,据此求出k的取值范围;
(2)首先求出k的最小整数,然后利用根与系数的关系求出代数式的值.
解答 解:(1)∵关于x的方程(k-1)x2+2x-5=0有两个实数根,
∴△≥0且k-1≠0,即4+20(k-1)≥0且k-1≠0,
∴k≥$\frac{4}{5}$且k≠1;
(2)∵k是满足条件的整数,
∴k=2,
∵a、b是方程x2+2x-5=0的两个实数根,
∴a2+2a-5=0,ab=-5,
∴a2+2a=5,
∴a2+5ab+2a=5+5×(-5)=-20.
点评 本题主要考查了根的判别式的知识,解答本题的关键是根据根的判别式的意义求出k的取值范围,此题难度不大.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:初中数学 来源: 题型:填空题
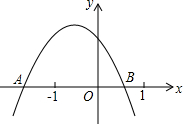 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,图象与x轴交于A(x1,0)B(x2,0)两点,点M(x0,y0)是图象上另一点,且x0>1.现有以下结论:①abc>0;②b<2a;③a+b+c>0;④a(x0-x1)(x0-x2)<0.
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,图象与x轴交于A(x1,0)B(x2,0)两点,点M(x0,y0)是图象上另一点,且x0>1.现有以下结论:①abc>0;②b<2a;③a+b+c>0;④a(x0-x1)(x0-x2)<0.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
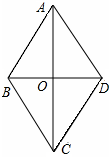 已知:如图,菱形ABCD的四边相等,且对角线互相垂直平分.在菱形ABCD中,对角线AC、DB相交于点O,且AC≠BD,则图中全等三角形有( )
已知:如图,菱形ABCD的四边相等,且对角线互相垂直平分.在菱形ABCD中,对角线AC、DB相交于点O,且AC≠BD,则图中全等三角形有( )| A. | 7对 | B. | 8对 | C. | 9对 | D. | 10对 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{a}$+$\frac{2}{b}$=$\frac{3}{a+b}$ | B. | $\frac{a}{-a+b}=-\frac{a}{a+b}$ | C. | $\frac{ab}{ab-{b}^{2}}=\frac{a}{a-b}$ | D. | $\frac{2}{2a+b}=\frac{1}{a+b}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
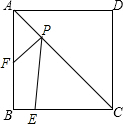 如图,正方形ABCD的边长为4,E为BC上的一点,BE=1,F为AB上的一点,AF=2,P为AC上一个动点,则PF+PE的最小值为$\sqrt{17}$.
如图,正方形ABCD的边长为4,E为BC上的一点,BE=1,F为AB上的一点,AF=2,P为AC上一个动点,则PF+PE的最小值为$\sqrt{17}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com