
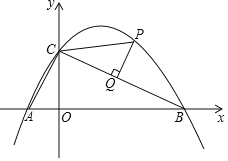
【题目】如图,二次函数![]() 的图像与
的图像与![]() 轴相交于点A(-1,0),B(4,0),与
轴相交于点A(-1,0),B(4,0),与![]() 轴相交于点C.
轴相交于点C.
(1)求该函数的表达式;
(2)若点P(2,m)为该函数在第一象限内的图象上一点,过点P作PQ⊥BC,垂足为点Q,连接PC,求线段PQ的长;
(3)在(2)的条件下,点M为该函数图象上一点,且∠MAP=45°,求点M的坐标.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)(4,0).
;(3)(4,0).
【解析】
(1)把点A、B代入二次函数的解析式,求出a、b的值,即可得到答案;
(2)作PN⊥x轴与N,交BC于点G,先求出点P和点C,然后得到直线BC的解析式,从而得到点N和点G的坐标,得到PG的长度,然后利用△PQG∽△BOC,即可求出PQ的长度;
(3)连接AP,则得到△APN是等腰直角三角形,则∠PAN=45°,则点M与点B重合,即可得到点M的坐标.
解:(1)根据题意,把点A、B代入抛物线![]() ,得
,得
![]() ,
,
解得: ,
,
∴二次函数的解析式为:![]() ;
;
(2)如图,作PN⊥x轴与N,交BC于点G,
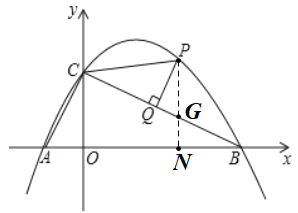
∵点P(2,m)在抛物线上,则
![]() ,
,
令x=0,则y=2,
∴点P为(2,3),点C为(0,2),点N为(2,0),
设直线BC为![]() ,则
,则
![]() ,解得:
,解得: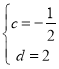 ,
,
∴直线BC的解析式为:![]() ;
;
令![]() ,
,![]() ,
,
∴点G的坐标为:(2,1),
∴PG=2,
∵OC∥PN,PQ⊥BC,
∴∠OCB=∠PGQ,∠BOC=∠PQG=90°,
∴△PQG∽△BOC,
∴![]() ,
,
∵BO=4,PG=2,![]() ,
,
∴![]() ;
;
(3)如图,连接AP,
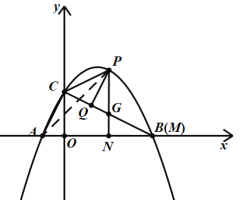
由(2)可知,点P为(2,3),点N为(2,0),点A为(-1,0),
∴AN=PN=3,
∵PN⊥AN,
∴△APN是等腰直角三角形,
∴∠PAN=45°,
∵点M在抛物线上,且∠MAP=45°,
∴点M与点B重合,此时点M的坐标为(4,0);
∴点M的坐标为:(4,0).


科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-(m+2)x+(2m-1)=0。
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长。
查看答案和解析>>
科目:初中数学 来源: 题型:
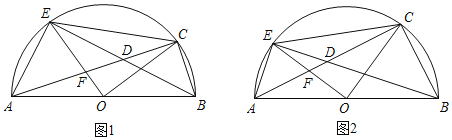
【题目】如图,AB是半圆O的直径,C为半圆弧上一点,在AC上取一点D,使BC=CD,连结BD并延长交⊙O于E,连结AE,OE交AC于F.
(1)求证:△AED是等腰直角三角形;
(2)如图1,已知⊙O的半径为![]() .
.
①求![]() 的长;
的长;
②若D为EB中点,求BC的长.
(3)如图2,若AF:FD=7:3,且BC=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料,并完成相应的任务.
在数学中,当问题的条件不够时间,常添加辅助线构成新图形,形成新关系,建立已知与未知的桥梁,从而把原问题转化为易于解决的问题.在著名美籍匈牙利数学教波利亚所著的《数学的发现》一书中有这样一个例子:试作一个三角形,使它的三边长分别是各条中线长的三分之一,解决这个问题的步骤如下:

第一步,如图1,己知![]() 的三条中线
的三条中线![]() ,
,![]() 和
和![]() 相交于点
相交于点![]() ,则有
,则有![]() .
.
下面是该结论的部分证明过程:

证明:如图1,过点![]() 作
作![]() 的平分线,交
的平分线,交![]() 的延长线于点
的延长线于点![]() ,则
,则![]() .
.
又![]() ,
,
∴![]() .
.
∴![]() .
.
∵点![]() 是
是![]() 的中点,
的中点,
∴![]() .
.
……
第二步,同理可以证明:![]() .
.
第三步,如图2,取BM的中点![]() ,连接
,连接![]() .则
.则![]() 的三边长分别是各条中线长的三分之一.
的三边长分别是各条中线长的三分之一.
任务:(1)请在上面第一步中证明过程的基础上完成对结论![]() 的证明;
的证明;
(2)请完成第三步的结论的证明;
(3)请直接写出图2中![]() 与
与![]() 的面积比:
的面积比:![]() _______.
_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的函数y=![]() +x,如表是y与x的几组对应值:
+x,如表是y与x的几组对应值:
x | … | ﹣4 | ﹣3 | -2 | - | -1 | - | - |
|
| 1 |
| 2 | 3 | 4 | … |
y | … | - | - | - | - | -2 | - | - |
|
| 2 |
|
|
|
| … |
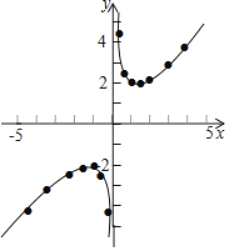
如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点画出了此函数的图象请你根据学习函数的经验,根据画出的函数图象特征,对该函数的图象与性质进行探究:
(1)该函数的图象关于 对称;
(2)在y轴右侧,函数变化规律是当0<x<1,y随x的增大而减小;当x>1,y随x的增大而增大.在y轴左侧,函数变化规律是 .
(3)函数y=![]() 当x 时,y有最 值为 .
当x 时,y有最 值为 .
(4)若方程![]() +x=m有两个不相等的实数根,则m的取值范围是 .
+x=m有两个不相等的实数根,则m的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
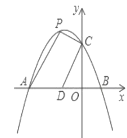
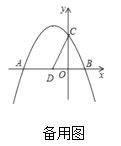
【题目】如图,抛物线![]() 交
交![]() 轴于点
轴于点![]() 和点
和点![]() ,交
,交![]() 轴于点
轴于点![]() .已知点
.已知点![]() 的坐标为
的坐标为![]() ,点
,点![]() 为第二象限内抛物线上的一个动点,连接
为第二象限内抛物线上的一个动点,连接![]() 、
、![]() 、
、![]() .
.
(1)求这个抛物线的表达式.
(2)当四边形![]() 面积等于4时,求点
面积等于4时,求点![]() 的坐标.
的坐标.
(3)①点![]() 在平面内,当
在平面内,当![]() 是以
是以![]() 为斜边的等腰直角三角形时,直接写出满足条件的所有点
为斜边的等腰直角三角形时,直接写出满足条件的所有点![]() 的坐标;
的坐标;
②在①的条件下,点![]() 在抛物线对称轴上,当
在抛物线对称轴上,当![]() 时,直接写出满足条件的所有点
时,直接写出满足条件的所有点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com