
【题目】如图,在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 的高
的高![]() 与角平分线
与角平分线![]() 相交点
相交点![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,交
,交![]() 于
于![]() .下列说法:①
.下列说法:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .正确的是_____.
.正确的是_____.

【答案】①③⑤
【解析】(1)∵CH⊥AE于点G,∠ACB=90°,
∴∠CGE=∠ACB=90°,
∴∠BCH+∠CEA=∠CEA+∠CAE=90°,
∴∠CAE=∠BCH;(故说法①成立)
(2)如下图,连接BF,过点F作FN⊥BC于点N,

∵AB=AC,AD是高,
∴AD平分∠ACB,
又∵AE平分∠BAC,且AE交CD于点F,
∴BF平分∠ABC,
∴DF=NF,
又∵NF<EF,
∴DF<EF;(故说法②错误)
(3)∵AC=BC,∠ACB=90°,CD是△ABC的高,
∴∠ACF=∠CBH=45°,
又∵由(1)可知∠CAE=∠BCH,
∴△CAF≌△BCH,
∴CF=BH.
∵∠CAE=∠BAE,∠ACE=∠ADF=90°,
∴∠CEF=∠AFD=∠CFE,
∴CE=CF,
∴CE=BH;(故说法③正确)
(4)如下图,过点E作EM⊥AB于点M,
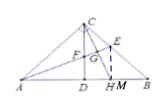
∵AE平分∠BAC,∠ACB=90°,
∴EM=EC,
∵AC=BC,∠ACB=90°,
∴AB=![]() AC,
AC,
∵S△ACE=![]() AC·CE,S△ABE=
AC·CE,S△ABE=![]() AB·EM,
AB·EM,
∴S△ABE=![]() S△ACE;(故说法④错误)
S△ACE;(故说法④错误)
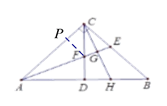
(5)如下图,过点F作FP⊥AC于点P,
∵CD是△ABC的高,AF平分∠BAC,
∴FP=FD,
∴S△ACF :S△ADF=AC:AD,
∵AC=BC,∠ACB=90°,CD是△ABC的高,
∴AC:AD=![]() ,
,
又∵S△ACF=![]() CF·AD,S△ADF=
CF·AD,S△ADF=![]() DF·AD,
DF·AD,
∴CF:DF= S△ACF :S△ADF=AC:AD=![]() ,
,
∴CF=![]() DF;(故说法⑤正确)
DF;(故说法⑤正确)
综上所述,正确的说法是①③⑤.
故答案为:①③⑤.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于A,B两点,B点坐标为(3,0).与y轴交于点C(0,3).
与x轴交于A,B两点,B点坐标为(3,0).与y轴交于点C(0,3).
(1)求抛物线的解析式;
(2)点P在x轴下方的抛物线上,过点P的直线y=x+m与直线BC交于点E,与y轴交于点F,求PE+EF的最大值;
(3)点D为抛物线对称轴上一点.
①当△BCD是以BC为直角边的直角三角形时,求点D的坐标;
②若△BCD是锐角三角形,求点D的纵坐标的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广.为了传承中华民族优秀传统文化,我市某中学举行“汉字听写”比赛,赛后整理参赛学生的成绩,将学生的成绩分为A,B,C,D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图,但均不完整.

请你根据统计图解答下列问题:
(1)参加比赛的学生共有____名;
(2)在扇形统计图中,m的值为____,表示“D等级”的扇形的圆心角为____度;
(3)组委会决定从本次比赛获得A等级的学生中,选出2名去参加全市中学生“汉字听写”大赛.已知A等级学生中男生有1名,请用列表法或画树状图法求出所选2名学生恰好是一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小康中学七年级(1)班学生进行拔河比赛分组,若每组 7 人,则有 2 人分不到组里;若每组 8 人,则最后一组差 4 人,若设计划分 x 组,则可列方程为( )
A.7 x 2 8x 4B.7 x 2 8x 4
C.7 x 2 8x 4D.7 x 2 8x 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:某礼品制造工厂接受一批玩具熊的订货任务,按计划天数生产,如果每天生产20个玩具熊,则比订货任务少100个;如果每天生产23个玩具熊,则可以超过订货任务20个.请求出该厂计划几天完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过∠AOB的平分线上一点C作CD∥OB交OA于点D,E是线段OC的中点,过点E作直线分别交射线CD,OB于点M,N,探究线段OD,ON,DM之间的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列语句中正确的是( )
A.两点之间直线的长度叫做这两点间的距离
B.两点之间的线段叫做这两点之间的距离
C.两点之间线的长度叫做这两点间的距离
D.两点之间线段的长度叫做这两点间的距离
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com