【题目】如图，抛物线与x轴交于A，B两点，B点坐标为（3，0）．与y轴交于点C（0，3）．

（1）求抛物线的解析式；

（2）点P在x轴下方的抛物线上，过点P的直线y=x+m与直线BC交于点E，与y轴交于点F，求PE+EF的最大值；

（3）点D为抛物线对称轴上一点．

①当△BCD是以BC为直角边的直角三角形时，求点D的坐标；

②若△BCD是锐角三角形，求点D的纵坐标的取值范围．

参考答案：

【答案】（1）；（2）；（3）①D点坐标为（2，5）或（2，﹣1）；②点D的纵坐标的取值范围为＜y＜5或﹣1＜y＜．

【解析】试题分析：（1）利用待定系数法求抛物线的解析式；

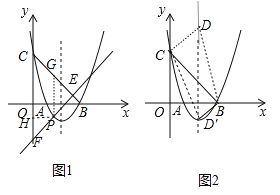
（2）易得BC的解析式为y=﹣x+3，先证明△ECF为等腰直角三角形，作PH⊥y轴于H，PG∥y轴交BC于G，如图1，则△EPG为等腰直角三角形，PE=PG，设P（t，t2﹣4t+3）（1＜t＜3），则G（t，﹣t+3），接着利用t表示PF、PE，所以PE+EF=2PE+PF= ，然后利用二次函数的性质解决问题；

（3）①如图2，抛物线的对称轴为直线x=2，设D（2，y），利用两点间的距离公式得到BC2=18，DC2=4+（y﹣3）2，BD2=1+y2，讨论：当△BCD是以BC为直角边，BD为斜边的直角三角形时，18+4+（y﹣3）2=1+y2；当△BCD是以BC为直角边，CD为斜边的直角三角形时，4+（y﹣3）2=1+y2+18，分别解方程求出t即可得到对应的D点坐标；

②由于△BCD是以BC为斜边的直角三角形有4+（y﹣3）2+1+y2=18，解出y的值，得到此时D点的坐标，然后结合图形可确定△BCD是锐角三角形时点D的纵坐标的取值范围．

试题解析：解：（1）把B（3，0），C（0，3）代入得： ，解得： ，∴抛物线的解析式为；

（2）易得BC的解析式为y=﹣x+3，∵直线y=x﹣m与直线y=x平行，∴直线y=﹣x+3与直线y=x﹣m垂直，∴∠CEF=90°，∴△ECF为等腰直角三角形，作PH⊥y轴于H，PG∥y轴交BC于G，如图1，△EPG为等腰直角三角形，PE=PG，设P（t，t2﹣4t+3）（1＜t＜3），则G（t，﹣t+3），∴PF=PH=t，PG=﹣t+3﹣（t2﹣4t+3）=﹣t2+3t，∴PE=PG= ，∴PE+EF=PE+PE+PF=2PE+PF= = =，当t=2时，PE+EF的最大值为；

（3）①如图2，抛物线的对称轴为直线x==2，设D（2，y），则BC2=32+32=18，DC2=4+（y﹣3）2，BD2=（3﹣2）2+y2=1+y2，当△BCD是以BC为直角边，BD为斜边的直角三角形时，BC2+DC2=BD2，即18+4+（y﹣3）2=1+y2，解得y=5，此时D点坐标为（2，5）；

当△BCD是以BC为直角边，CD为斜边的直角三角形时，BC2+DB2=DC2，即4+（y﹣3）2=1+y2+18，解得y=﹣1，此时D点坐标为（2，﹣1）；

综上所述：D点坐标为（2，5）或（2，﹣1）．

②当△BCD是以BC为斜边的直角三角形时，DC2+DB2=BC2，即4+（y﹣3）2+1+y2=18，解得y1=，y2=，此时D点坐标为（2， ）或（2， ），所以△BCD是锐角三角形，点D的纵坐标的取值范围为＜y＜5或﹣1＜y＜．

关闭