【题目】某玩具厂有4个车间，某周是质量检查周，现每个车间都原有a（a>0）个成品，且每个车间每天都生产b（b>0）个成品，质量科派出若干名检验员周一、周二检验其中两个车间原有的和这两天生产的所有成品，然后，周三到周五检验另外两个车间原有的和本周生产的所有成品，假定每名检验员每天检验的成品数相同．
（1）这若干名检验员1天共检验多少个成品?（用含a、b的代数式表示）
（2）若一名检验员1天能检验
b个成品，则质量科至少要派出多少名检验员?
【答案】(1) a+2b或
;(2) 至少要派8名检验员．
【解析】试题分析：（1）求得两个车间星期一和星期二两天共生产的数量，再加上原有的2a个，得质检员两天共检查的数量，除以2即1天的检查数量.或求得另外两个车间星期三至星期五三天共生产的数量，再加上原有的2a+4b个，得质检员三天共检查的数量，除以3即1天的检查数量.或求得星期一至星期五质检员总共检查的数量，再除以5即1天的检查数量；（2）根据（1）中前两天求得的1天检查的数量等于后三天求得的1天检查的数量，便可求得；（3）设质检科要派出x名检验员，则x名质检员1天最多能检查
bx个，得a+2b≤bx，将a=4b代入，便可求出.
试题解析：(1)这若干名检验员1天能检验的个数为（2a+4b）÷2＝a＋2b或（2a+4b+6b）÷3=
或（4a+4b+10b）÷5=
.
(2)根据题意，得a＋2b=，得a＝4b.
(3)设质检科要派出x名检验员，
根据题意，得a+2b≤bx，
将a=4b代入，得4b+2b≤bx,解得x≥7.5.
由x为正整数，则x最小为8.
答：质检科至少要派出8名检验员．
寒假创新型自主学习第三学期寒假衔接系列答案科目：初中数学 来源： 题型：
【题目】如图，在四边形ABCD中，∠DAB=∠ABC=90
,AD∥BC,AB=BC,E是AB的中点，CE⊥BD.
(1)求证：BE=AD；
(2)求证：AC是线段ED的垂直平分线;
(3)△DBC是等腰三角形吗？并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】画图并填空：如图，方格纸中每个小正方形的边长都为1．在方格纸内将△ABC经过一次平移后得到△A′B′C′，图中标出了点B的对应点B′．
（1）在给定方格纸中画出平移后的△A′B′C′；
利用网格点和三角板画图或计算：
（2）画出AB边上的中线CD；
（3）画出BC边上的高线AE；
（4）△A′B′C′的面积为______．
【答案】（1）作图见解析；（2）作图见解析；（3）作图见解析；（4）8.
【解析】解:(1)如图所示: 
即为所求;
(2)如图所示:CD就是所求的中线;
(3)如图所示:AE即为BC边上的高;
(4)
.
故的面积为8.
因此，本题正确答案是:8.
【题型】解答题
【结束】
24
【题目】如图，⊿ABC中，∠A=40°，∠ACB=104°，BD为AC边上的高，BE是⊿ABC的角平分线，求∠EBD的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
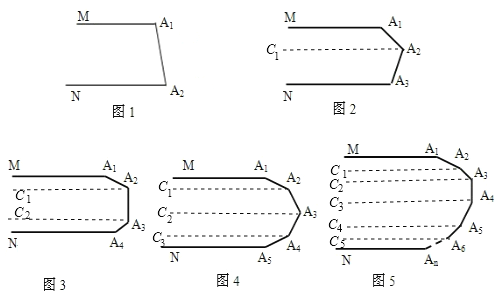
【题目】(1) 如图1，MA1∥NA2，则∠A1+∠A2=_________度．
如图2，MA1∥NA3，则∠A1+∠A2+∠A3=_________ 度．
如图3，MA1∥NA4，则∠A1+∠A2+∠A3+∠A4=_________度．
如图4，MA1∥NA5，则∠A1+∠A2+∠A3+∠A4+∠A5=_________度．
如图5，MA1∥NAn，则∠A1+∠A2+∠A3+…+∠An=_________ 度．
(2) 如图,已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E=80°，求∠BFD的度数.
【答案】（1） 180； 360； 540；720；180（n-1）；（2）140°.
【解析】试题分析：（1）首先过各点作MA 1 的平行线，由MA 1 ∥NA 2 ，可得各线平行，根据两直线平行，同旁内角互补，即可求得答案；
（2）由（1）中的规律可得∠ABE+∠E+∠CDE=360°，所以∠ABE+∠CDE=360°-80°=280°，又因为BF、DF平分∠ABE和∠CDE，所以∠FBE+∠FDE=140°，又因为四边形的内角和为360°，进而可得答案．
试题解析：（1）如图1，
∵MA 1 ∥NA 2 ，
∴∠A 1 +∠A 2 =180°．
如图2，过点A 2 作A 2 C 1 ∥A 1 M，
∵MA 1 ∥NA 3 ，
∴A 2 C 1 ∥A 1 M∥NA 3 ，
∴∠A 1 +∠A 1 A 2 C 1 =180°，∠C 1 A 2 A 3 +∠A 3 =180°，
∴∠A 1 +∠A 2 +∠A 3 =360°．
如图3，过点A 2 作A 2 C 1 ∥A 1 M，过点A 3 作A 3 C 2 ∥A 1 M，
∵MA 1 ∥NA 3 ，
∴A 2 C 1 ∥A 3 C 2 ∥A 1 M∥NA 3 ，
∴∠A 1 +∠A 1 A 2 C 1 =180°，∠C 1 A 2 A 3 +∠A 2 A 3 C 2 =180°，∠C 2 A 3 A 4 +∠A 4 =180°，
∴∠A 1 +∠A 2 +∠A 3 +∠A 4 =540°．
如图4，过点A 2 作A 2 C 1 ∥A 1 M，过点A 3 作A 3 C 2 ∥A 1 M，
∵MA 1 ∥NA 3 ，
∴A 2 C 1 ∥A 3 C 2 ∥A 1 M∥NA 3 ，
∴∠A 1 +∠A 1 A 2 C 1 =180°，∠C 1 A 2 A 3 +∠A 2 A 3 C 2 =180°，∠C 2 A 3 A 4 +∠A 3 A 4 C 3 =180°，∠C 3 A 4 A 5 +∠A 5 =180°，
∴∠A 1 +∠A 2 +∠A 3 +∠A 4 +∠A 5 =720°；
从上述结论中你发现了规律：如图5，MA 1 ∥NA n ，则∠A 1 +∠A 2 +∠A 3 +…+∠A n =180（n-1）度，
故答案为：180，360，540，720，180（n-1）；
（2）由（1）可得∠ABE+∠E+∠CDE=360°，
∵∠E=80°，
∴∠ABE+∠CDE=360°-80°=280°，
又∵BF、DF平分∠ABE和∠CDE，
∴∠FBE+∠FDE=140°，
∵∠FBE+∠E+∠FDE+∠BFD=360°，
∴∠BFD=360°-80°-140°=140°．
【点睛】本题考查了平行线的性质：两直线平行，同旁内角互补、四边形的内角和是360°，解题的关键是，（1）小题正确添加辅助线，发现规律：MA 1 ∥NA n ，则∠A 1 +∠A 2 +∠A 3 +…+∠A n =180（n-1）度；（2）小题能应用（1）中发现的规律.
【题型】解答题
【结束】
28
【题目】已知如图1，线段AB、CD相交于点O，连结AC、BD，我们把形如图1的图形称之为“8字形”，那么在这一个简单的图形中，到底隐藏了哪些数学知识呢？下面就请你发挥聪明才智，解决以下问题：
(1)在图1中，请写出∠A、∠B、∠C、∠D之间的数量关系，并说明理由；
(2)仔细观察，在图2中“8字形”的个数有 个；
(3)在图2中，若∠B＝76°，∠C＝80°，∠CAB和∠BDC的平分线AP和DP相交于点P，并且与CD、AB分别相交于M、N利用(1)的结论，试求∠P的度数；
(4)在图3中，如果∠B和∠C为任意角，并且AP和DP分别是∠CAB和∠BDC的三等分线，即∠PAO＝
∠CAO， ∠BDP＝
∠BOD，那么∠P与∠C、∠B之间存在的数量关系是 （直接写出结论即可）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我国西南五省市的部分地区发生严重旱灾，为鼓励节约用水，某市自来水公司采取分段收费标准，右图反映的是每月收取水费y（元）与用水量x（吨）之间的函数关系．
（1）小明家五月份用水8吨，应交水费______ 元；
（2）按上述分段收费标准，小明家三、四月份分别交水费26元和18元，问四月份比三月份节约用水多少吨？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线
与x轴交于A，B两点，B点坐标为（3，0）．与y轴交于点C（0，3）．
（1）求抛物线的解析式；
（2）点P在x轴下方的抛物线上，过点P的直线y=x+m与直线BC交于点E，与y轴交于点F，求PE+EF的最大值；
（3）点D为抛物线对称轴上一点．
①当△BCD是以BC为直角边的直角三角形时，求点D的坐标；
②若△BCD是锐角三角形，求点D的纵坐标的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，过∠AOB的平分线上一点C作CD∥OB交OA于点D，E是线段OC的中点，过点E作直线分别交射线CD，OB于点M，N，探究线段OD，ON，DM之间的数量关系，并证明你的结论．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com