练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】列方程或方程组解应用题：

    某校为美化校园，计划对一些区域进行绿化，安排了甲、乙两个工程队完成，已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍，并且两队在独立完成面积为400m2区域的绿化时，甲队比乙队少用4天，求甲、乙两工程队每天能完成绿化的面积分别是多少m2？

    【答案】甲、乙两工程队每天能完成绿化的面积分别是100m2、50m2．

    【解析】试题分析：设乙工程队每天能完成绿化的面积是xm2，根据在独立完成面积为400m2区域的绿化时，甲队比乙队少用4天，列出分式方程，解方程即可．

    试题解析：设乙工程队每天能完成绿化的面积是xm2，

    根据题意得： ，

    解得：x=50．

    经检验：x=50是原方程的解．

    所以甲工程队每天能完成绿化的面积是50×2=100（m2）．

    答：甲、乙两工程队每天能完成绿化的面积分别是100m2、50m2．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，平行四边形ABCD中，AF、CE分别是∠BAD和∠BCD的角平分线，根据现有的图形，请添加一个条件，使四边形AECF为菱形，则添加的一个条件可以是 ． （只需写出一个即可，图中不能再添加别的“点”和“线”）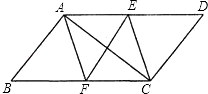

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】平面直角坐标系中，点P的坐标为（﹣5，3），则点P关于原点对称的点的坐标是（　　）

    A. （5，﹣3） B. （﹣5，﹣3） C. （3，﹣5） D. （﹣3，5）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D,下面四个结论:①∠ABE=∠BAD;②△CEB≌△ADC;③AB=CE;④AD-BE=DE.其中正确的是 (将你认为正确结论的序号都写上).

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,在△ABC中,∠BAC=∠ABC,点P在AB上,如果AD⊥CP,BE⊥CP的延长线,垂足分别为D,E,且BE=CD.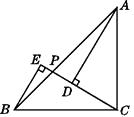

    （1）试探求这个图形中还有哪些相等的线段,并给出证明;
    （2）试确定△ABC的形状.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在同一个平面内，不重合的两条直线的位置关系是（　　）
    A.平行
    B.相交
    C.平行或相交
    D.无法确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：

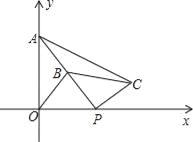
    【题目】如图，在平面直角坐标系中，点A的坐标为（0，2），点P（t，0）在x轴上，B是线段PA的中点．将线段PB绕着点P顺时针方向旋转90°，得到线段PC，连结OB、BC．

    （1）判断△PBC的形状，并简要说明理由；

    （2）当t＞0时，试问：以P、O、B、C为顶点的四边形能否为平行四边形？若能，求出相应的t的值？若不能，请说明理由；

    （3）当t为何值时，△AOP与△APC相似？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列说法正确的是（　　）

    A. 在Rt△ABC中，∠C=90°，若tanA= ，则a=3，b=4

    B. 若△ABC三边之比为1： ，且∠A为最小角，则sinA=

    C. 对于锐角α，必有sinα＞cosα

    D. 在Rt△ABC中，若∠C=90°，则sin2A+cos2A=1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】把所有正奇数从小到大排列，并按如下规律分组：（1），（3，5，7），（9，11，13，15，17），（19，21，23，25，27，29，31），…，现有等式Am=（i，j）表示正奇数m是第i组第j个数（从左往右数），如A7=（2，3），则A2015=（　　）

    A. （31，50） B. （32，47） C. （33，46） D. （34，42）

    查看答案和解析>>

    同步练习册答案