
【题目】如图,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D,下面四个结论:①∠ABE=∠BAD;②△CEB≌△ADC;③AB=CE;④AD-BE=DE.其中正确的是 (将你认为正确结论的序号都写上).
【答案】①②④
【解析】解: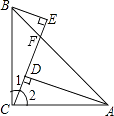
∵BE⊥CE于点E,AD⊥CE于点D ,
∴ ∠BEF=∠ADF=90°,
又∵∠BFE=∠AFD
∴∠ABE=∠BAD ;故 ① 正确
∵∠1+∠2=90° ,∠2+∠CAD=90°
∴∠1=∠CAD ,
又∠E=∠ADC=90°,AC=BC
∴△CEB≌△ADC (AAS), 故 ②正确
∴CE=AD,BE=CD
∴AD-BE=DE , 故 ④ 正确;
而③不能证明,
故答案为 :①、②、④
根据垂直的定义得出∠BEF=∠ADF=90° ,根据等顶角相等及三角形的内角和得出∠ABE=∠BAD ;故 ① 正确 ;根据同角的余角相等得出∠1=∠CAD ,从而利用AQAS判断出△CEB≌△ADC ,故 ②正确;根据全等三角形对应边相等得出CE=AD,BE=CD ,根据等式的性质得出AD-BE=DE , 故 ④ 正确; 从而得出答案。


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB= ![]() ,点E、F分别在BC、CD上,且∠BAE=30°,∠DAF=15度.
,点E、F分别在BC、CD上,且∠BAE=30°,∠DAF=15度.
(1)求证:DF+BE=EF;
(2)求∠EFC的度数;
(3)求△AEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A,B的坐标分别为(1,0),(0,2),若将线段AB平移到A1B1,点A1,B1的坐标分别为(2,a),(b,3),则a22b的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,H是△ABC的高AD,BE的交点,且DH=DC,则下列结论:①BD=AD;②BC=AC;③BH=AC;④CE=CD中,正确的有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
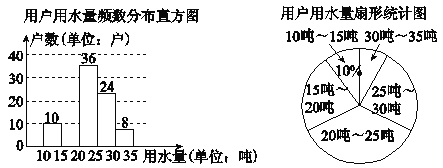
【题目】某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行超价收费,为更好地决策,自来水公司随机抽取了部分用户的用水量数据,并绘制了如图不完整的统计图(每组数据包括右端点但不包括左端点),请你根据统计图解答下列问题:
(1)此次抽样调查的样本容量是________;
(2)补全频数分布直方图,求扇形图中“15吨~20吨”部分的圆心角的度数;
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题:
某校为美化校园,计划对一些区域进行绿化,安排了甲、乙两个工程队完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且两队在独立完成面积为400m2区域的绿化时,甲队比乙队少用4天,求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正比例函数y=kx经过点A , 点A在第四象限,过点A作AH⊥x轴,垂足为点H , 点A的横坐标为3,且△AOH的面积为3.
(1)求正比例函数的解析式;
(2)在x轴上能否找到一点P , 使△AOP的面积为5?若存在,求点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励大众创业,万众创新,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=﹣10x+500.
(1)李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于3000元,那么政府为他承担的总差价最少为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com