
【题目】如图,正方形ABCD中,AB= ![]() ,点E、F分别在BC、CD上,且∠BAE=30°,∠DAF=15度.
,点E、F分别在BC、CD上,且∠BAE=30°,∠DAF=15度.
(1)求证:DF+BE=EF;
(2)求∠EFC的度数;
(3)求△AEF的面积.
【答案】
(1)证明:延长EB至G,使BG=DF,连接AG,
∵正方形ABCD,
∴AB=AD,∠ABG=∠ADF=∠BAD=90°,
∵BG=DF,
∴△ABG≌△ADF,
∴AG=AF,
∵∠BAE=30°,∠DAF=15°,
∴∠FAE=∠GAE=45°,
∵AE=AE,
∴△FAE≌△GAE,
∴EF=EG=GB+BE=DF+BE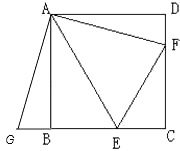
(2)解:∵△AGE≌△AFE,
∴∠AFE=∠AGE=75°,
∵∠DFA=90°-∠DAF=75°,
∴∠EFC=180°-∠DFA-∠AFE=180°-75°-75°=30°,
∴∠EFC=30°
(3)解:∵AB=BC= ![]() ,∠BAE=30°,
,∠BAE=30°,
∴BE=1,CE= ![]() -1,
-1,
∵∠EFC=30°,
∴CF=3- ![]() ,
,
∴S△CEF= ![]() CECF=2
CECF=2 ![]() -3,
-3,
由(1)知,△ABG≌△ADF,△FAE≌△GAE,
∴S△AEF=S正方形ABCD-S△ADF-S△AEB-S△CEF=S正方形ABCD-S△AEF-S△CEF ,
S△AEF= ![]() (S正方形ABCD-S△AEF-S△CEF)=3-
(S正方形ABCD-S△AEF-S△CEF)=3- ![]()
【解析】(1)根据已知条件可证△ABG≌△ADF,可得AG=AF,然后可证△FAE≌△GAE,则结论可得;(2)由(1)知,△FAE≌△GAE,结合已知条件可得解;(3)根据![]() AEF的面积=正方形ABCD的面积-
AEF的面积=正方形ABCD的面积-![]() ADF的面积-
ADF的面积-![]() AEB的面积-
AEB的面积-![]() CEF的面积=正方形ABCD的面积-
CEF的面积=正方形ABCD的面积-![]() AEF的面积-
AEF的面积-![]() CEF的面积即可求解。
CEF的面积即可求解。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】标号为A、B、C、D的四个盒子中所装有白球和黑球数如下,则下列盒子最易摸到黑球的是( )
A.9个黑球和3个白球 B.10黑球和10个白球
C.12个黑球和6个白球 D.10个黑球和5个白球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为a的正方形ABCD和边长为b的正方形BEFG排放在一起,O1和O2分别是两个正方形的中心,则阴影部分的面积为 , 线段O1O2的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段a、b。![]()
求作:(1)Rt△ABC,使![]()
(2)△ABC的角平分线CD和经过点A、C、D的⊙O.(作CD和⊙O不要求写作法,但要保留作图痕迹)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AF、CE分别是∠BAD和∠BCD的角平分线,根据现有的图形,请添加一个条件,使四边形AECF为菱形,则添加的一个条件可以是 . (只需写出一个即可,图中不能再添加别的“点”和“线”)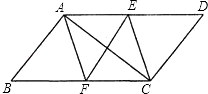
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某青年旅社有60间客房供游客居住,在旅游旺季,当客房的定价为每天200元时,所有客房都可以住满.客房定价每提高10元,就会有1个客房空闲,对有游客入住的客房,旅社还需要对每个房间支出20元/每天的维护费用,设每间客房的定价提高了x元.
(1)填表(不需化简)
入住的房间数量 | 房间价格 | 总维护费用 | |
提价前 | 60 | 200 | 60×20 |
提价后 |
|
|
|
(2)若该青年旅社希望每天纯收入为14000元且能吸引更多的游客,则每间客房的定价应为多少元?(纯收入=总收入﹣维护费用)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D,下面四个结论:①∠ABE=∠BAD;②△CEB≌△ADC;③AB=CE;④AD-BE=DE.其中正确的是 (将你认为正确结论的序号都写上).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com