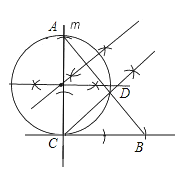
【题目】如图，已知线段a、b。
求作：（1）Rt△ABC，使
（2）△ABC的角平分线CD和经过点A、C、D的⊙O.（作CD和⊙O不要求写作法，但要保留作图痕迹）
【答案】见解析
【解析】试题分析：（1）先作两条互相垂直的直线，作出直角，确定直角顶点C，然后在以C为顶点的两条射线上截取CB=a，CA=b，连接AB即可得到所求作的直角三角形；
（2）①以C为圆心，任意长为半径作弧交CA、CB于两点，以这两点为圆心，大于两点间距离的一半为半径作弧，两弧交于一点（设此点为P），连接CP，CP与AB的交点即为点D，CD就是要求作的角平分线；
②作△ACD任意两边的垂直平分线，两条垂直平分线的交点即为圆心O，以O为圆心，OA为半径作圆，⊙O即为所求作的圆．
试题解析：
（1）①作直线
垂足为C；
②分别截取CB = a，CA = b；
③连结AB，则△ABC为所求作的三角形；
（2）正确作出CD，正确作出⊙O.
名校课堂系列答案科目：初中数学 来源： 题型：
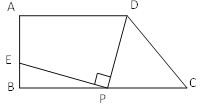
【题目】如图：梯形ABCD中，AD∥BC，∠ABC=90°，AD=9，BC=12，AB=6，在线段BC上任取一点P，连接DP，作射线PE⊥DP，PE与直线AB交于点E.
（1）试确定当CP=3时，点E的位置；
（2）若设CP=x，BE=y，试写出y关于自变量x的函数关系式.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD中，AB＝ 
，点E、F分别在BC、CD上，且∠BAE＝30°，∠DAF＝15度．
（1）求证：DF＋BE＝EF；
（2）求∠EFC的度数；
（3）求△AEF的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
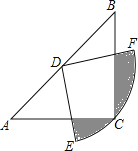
【题目】如图，在△ABC中，CA=CB，∠ACB=90°，以AB的中点D为圆心，作圆心角为90°的扇形DEF，点C恰在EF上，设∠BDF=α（0°＜α＜90°），当α由小到大变化时，图中阴影部分的面积（ ）
A. 由小到大 B. 由大到小 C. 不变 D. 先由小到大，后由大到小
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列命题中：①有公共顶点且相等的角是对顶角；②直线外一点到这条直线的垂线段，叫做点到直线的距离；③互为邻补角的两个角的平分线互相垂直；④经过一点有且只有一条直线与已知直线平行．其中真命题的个数有（ ）
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目：初中数学 来源： 题型：
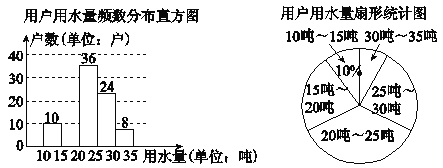
【题目】某市为提倡节约用水，准备实行自来水“阶梯计费”方式，用户用水不超出基本用水量的部分享受基本价格，超出基本用水量的部分实行超价收费，为更好地决策，自来水公司随机抽取了部分用户的用水量数据，并绘制了如图不完整的统计图(每组数据包括右端点但不包括左端点)，请你根据统计图解答下列问题：
(1)此次抽样调查的样本容量是________；
(2)补全频数分布直方图，求扇形图中“15吨～20吨”部分的圆心角的度数；
(3)如果自来水公司将基本用水量定为每户25吨，那么该地区6万用户中约有多少用户的用水全部享受基本价格？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com