
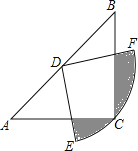
【题目】如图,在△ABC中,CA=CB,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰在EF上,设∠BDF=α(0°<α<90°),当α由小到大变化时,图中阴影部分的面积( )
A. 由小到大 B. 由大到小 C. 不变 D. 先由小到大,后由大到小
【答案】C
【解析】试题分析:作DM⊥AC于M,DN⊥BC于N,构造正方形DMCN,利用正方形和等腰直角三角形的性质,通过证明△DMG≌△DNH,把△DHN补到△DNG的位置,得到四边形DGCH的面积=正方形DMCN的面积,于是得到阴影部分的面积=扇形的面积﹣正方形DMCN的面积,即为定值.
试题解析:解:作DM⊥AC于M,DN⊥BC于N,连接DC,
∵CA=CB,∠ACB=90°,
∴∠A=∠B=45°,
DM=![]() AD=
AD=![]() AB,DN=
AB,DN=![]() BD=
BD=![]() AB,
AB,
∴DM=DN,
∴四边形DNCN是正方形,
∴∠MDN=90°,
∴∠MDG=90°﹣∠GDN,
∵∠EDF=90°,
∴∠NDH=90°﹣∠GDN,
∴∠MDG=∠NDH,
在△DMG和△DNH中,
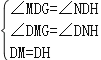 ,
,
∴△DMG≌△DNH,
∴四边形DGCH的面积=正方形DMCN的面积,
∵正方形DMCN的面积=DM2=![]() AB2,
AB2,
∴四边形DGCH的面积=![]() ,
,
∵扇形FDE的面积=![]() =
=![]() ,
,
∴阴影部分的面积=扇形面积﹣四边形DGCH的面积=![]() (定值),
(定值),
故选C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知线段a、b。![]()
求作:(1)Rt△ABC,使![]()
(2)△ABC的角平分线CD和经过点A、C、D的⊙O.(作CD和⊙O不要求写作法,但要保留作图痕迹)
查看答案和解析>>
科目:初中数学 来源: 题型:
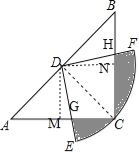
【题目】如图,四边形ABCD内接于⊙O,E为BC延长线上一点,∠A=50°,则∠DCE的度数为( )
A. 40° B. 50° C. 60° D. 130°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E,F分别为边AB,CD的中点,连接DE、BF、BD.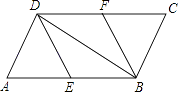
(1)求证:△ADE≌△CBF.
(2)若AD⊥BD,则四边形BFDE是什么特殊四边形?请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一块三角板ABC的直角顶点C放在直尺的一边PQ上,直尺的另一边MN与三角板的两边AC、BC分别交于两点E、D,且AD为∠BAC的平分线,∠B=300 , ∠ADE=150.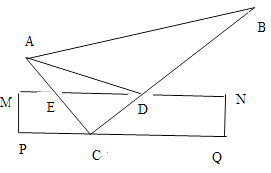
(1)求∠BDN的度数;
(2)求证:CD=CE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com