
【题目】如图,H是△ABC的高AD,BE的交点,且DH=DC,则下列结论:①BD=AD;②BC=AC;③BH=AC;④CE=CD中,正确的有( )
A.1个
B.2个
C.3个
D.4个
【答案】B
【解析】解:①∵BE⊥AC,AD⊥BC
∴∠AEH=∠ADB=90°
∵∠HBD+∠BHD=90°,∠EAH+∠AHE=90°,∠BHD=∠AHE
∴∠HBD=∠EAH
又∵DH=DC
∴△BDH≌△ADC(AAS)
∴BD=AD,BH=AC ;从而得出①③符合题意;
②:∵BC=AC
∴∠BAC=∠ABC
∵由①知,在Rt△ABD中,BD=AD
∴∠ABC=45°
∴∠BAC=45°
∴∠ACB=90°
∵∠ACB+∠DAC=90°,∠ACB<90°
②不符合题意;
解④:∵CE=CD ,∠ACB=∠ACB,∠ADC=∠BEC=90°,
∴△BEC≌△ADC
由于缺乏条件,无法证得△BEC≌△ADC
④不符合题意;
故应选:B.
根据垂直的定义得出∠AEH=∠ADB=90°,根据等顶角相等及等角的余角相等得出∠HBD=∠EAH,又DH=DC,从而利用AAS判断出△BDH≌△ADC,根据全等三角形对应边相等得出BD=AD,BH=AC ;根据等边对等角得出∠BAC=∠ABC,由等腰直角三角形的性质得出∠ABC=45°,根据等量代换得出∠BAC=45°,根据三角形的内角和得出∠ACB=90°,又∠ACB+∠DAC=90°,∠ACB<90°,从而得出②不符合题意;由于缺乏条件,无法证得△BEC≌△ADC,而要得出CE=CD,必须△BEC≌△ADC,故④不符合题意。


 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,边长为a的正方形ABCD和边长为b的正方形BEFG排放在一起,O1和O2分别是两个正方形的中心,则阴影部分的面积为 , 线段O1O2的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,点P的坐标为(﹣5,3),则点P关于原点对称的点的坐标是( )
A. (5,﹣3) B. (﹣5,﹣3) C. (3,﹣5) D. (﹣3,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC,D为BC的中点,以下结论:①△ABD≌△ACD;②AB=AC;③∠B=∠C;④AD是△ABC的角平分线.其中正确的有( )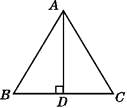
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D,下面四个结论:①∠ABE=∠BAD;②△CEB≌△ADC;③AB=CE;④AD-BE=DE.其中正确的是 (将你认为正确结论的序号都写上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=∠ABC,点P在AB上,如果AD⊥CP,BE⊥CP的延长线,垂足分别为D,E,且BE=CD.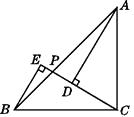
(1)试探求这个图形中还有哪些相等的线段,并给出证明;
(2)试确定△ABC的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标为(0,2),点P(t,0)在x轴上,B是线段PA的中点.将线段PB绕着点P顺时针方向旋转90°,得到线段PC,连结OB、BC.
(1)判断△PBC的形状,并简要说明理由;
(2)当t>0时,试问:以P、O、B、C为顶点的四边形能否为平行四边形?若能,求出相应的t的值?若不能,请说明理由;
(3)当t为何值时,△AOP与△APC相似?
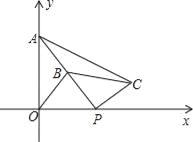
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,AB=4,AD=12,将矩形纸片折叠,使点C落在AD边上的点M处,折痕为PE,此时PD=3.在AB边上有一个动点F,且不与点A,B重合.当AF=______时,△MEF的周长最小。
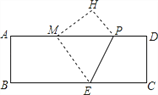
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com