练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】下列说法正确的是（　　）

    A. 在Rt△ABC中，∠C=90°，若tanA= ，则a=3，b=4

    B. 若△ABC三边之比为1： ，且∠A为最小角，则sinA=

    C. 对于锐角α，必有sinα＞cosα

    D. 在Rt△ABC中，若∠C=90°，则sin2A+cos2A=1

    【答案】D

    【解析】解：A. 在Rt△ABC中，∠C=90°，若tanA= ，则a=3x，b=4x，故A错误.

    B. 若△ABC三边之比为1： ，且∠A为最小角，则sinA=,故B错误.

    C. 对于α>45°，必有sinα＞cosα，当0<α<45°时，sinα<cosα，故C错误

    D. 在Rt△ABC中，若∠C=90°，则sin2A+cos2A=1，所以D选项是正确的.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】一件服装标价200元，若以6折销售，仍可获利20%，则这件服装的进价是（ ）
    A.100元
    B.105元
    C.108元
    D.118元

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】列方程或方程组解应用题：

    某校为美化校园，计划对一些区域进行绿化，安排了甲、乙两个工程队完成，已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍，并且两队在独立完成面积为400m2区域的绿化时，甲队比乙队少用4天，求甲、乙两工程队每天能完成绿化的面积分别是多少m2？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知正比例函数y=kx经过点A ， 点A在第四象限，过点A作AH⊥x轴，垂足为点H ， 点A的横坐标为3，且△AOH的面积为3．
    （1）求正比例函数的解析式；
    （2）在x轴上能否找到一点P ， 使△AOP的面积为5？若存在，求点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列运算错误的是( )
    A. =1
    B.x2+x2=2x4
    C.|a|=|-a|
    D. =

    查看答案和解析>>

    科目：初中数学 来源： 题型：

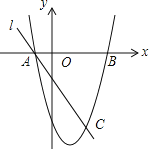
    【题目】（本题满分12分）如图，抛物线y=x2﹣2x﹣3与x轴交于A、B两点（A点在B点左侧），直线l与抛物线交于A、C两点，其中C点的横坐标为2．

    （1）求A、B、C三点的坐标；

    （2）在抛物线的对称轴上找到点P，使得△PBC的周长最小，并求出点P的坐标；

    （3）点G抛物线上的动点，在x轴上是否存在点F，使A、C、F、G为顶点四边形是平行四边形？如果存在，请直接写出F点坐标；如果不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，抛物线y=ax2+bx+c与直线y=﹣x+6分别交于x轴和y轴上同一点，交点分别是点B和点C，且抛物线的对称轴为直线x=4．

    （1）求出抛物线与x轴的两个交点A，B的坐标．

    （2）试确定抛物线的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为鼓励大众创业，万众创新，某市政府出台了相关政策：由政府协调，本市企业按成本价提供产品给大学毕业生自主销售，成本价与出厂价之间的差价由政府承担．李明按照相关政策投资销售本市生产的一种新型节能灯．已知这种节能灯的成本价为每件10元，出厂价为每件12元，每月销售量y（件）与销售单价x（元）之间的关系近似满足一次函数：y=﹣10x+500．
    （1）李明在开始创业的第一个月将销售单价定为20元，那么政府这个月为他承担的总差价为多少元？
    （2）设李明获得的利润为w（元），当销售单价定为多少元时，每月可获得最大利润？
    （3）物价部门规定，这种节能灯的销售单价不得高于25元．如果李明想要每月获得的利润不低于3000元，那么政府为他承担的总差价最少为多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,在△ABC中,分别与∠ABC,∠ACB相邻的外角的平分线相交于F,连接AF,下列结论正确的是( )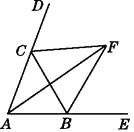

    A.AF平分BC
    B.AF平分∠BAC
    C.AF⊥BC
    D.以上结论都正确

    查看答案和解析>>

    同步练习册答案