
【题目】已知直线AB与CD相交于点O,且∠AOD=90°,现将一个直角三角尺的直角顶点放在点O处,把该直角三角尺OEF绕着点O旋转,作射线OH平分∠AOE.
(1)如图1所示,当∠DOE=20°时,∠FOH的度数是 .
(2)若将直角三角尺OEF绕点O旋转至图2的位置,试判断∠FOH和∠BOE之间的数量关系,并说明理由.
(3)若再作射线OG平分∠BOF,试求∠GOH的度数.

【答案】(1)35°;(2)∠BOE=2∠FOH,理由详见解析;(3)45°或135°.
【解析】
(1)根据∠AOD=90![]() ,∠DOE=20
,∠DOE=20![]() 得∠AOE=∠AOD+∠DOE=110
得∠AOE=∠AOD+∠DOE=110![]() ,再根据OH平分∠AOE,即可求解;
,再根据OH平分∠AOE,即可求解;
(2)可以设∠AOH=x,根据OH平分∠AOE,可得∠HOE=∠AOH=x,进而∠FOH=90![]() ﹣∠HOE=90
﹣∠HOE=90![]() ﹣x,∠BOE=180
﹣x,∠BOE=180![]() ﹣∠AOE=180
﹣∠AOE=180![]() ﹣2x,即可得结论;
﹣2x,即可得结论;
(3)分两种情况解答:当OE落在∠BOD内时,OF落在∠AOD内,当OE落在其他位置时,根据OH平分∠AOE,OG平分∠BOF即可求解.
解:(1)因为∠AOD=90![]() ,∠DOE=20
,∠DOE=20![]()
所以∠AOE=∠AOD+∠DOE=110![]()
因为OH平分∠AOE
所以∠HOE=![]() AOE=55
AOE=55![]()
所以∠FOH=90![]() ﹣∠HOE=35
﹣∠HOE=35![]() ;
;
故答案为35![]() ;
;
(2)∠BOE=2∠FOH,理由如下:
设∠AOH=x,
因为OH平分∠AOE
所以∠HOE=∠AOH=x
所以∠FOH=90![]() ﹣∠HOE=90
﹣∠HOE=90![]() ﹣x
﹣x
∠BOE=180![]() ﹣∠AOE=180
﹣∠AOE=180![]() ﹣2x
﹣2x
所以∠BOE=2∠FOH;
(3)如图3,当OE落在∠BOD内时,OF落在∠AOD内
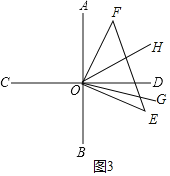
因为OH平分∠AOE
所以∠HOE=∠AOH=![]() AOE
AOE
因为OG平分∠BOF
∠FOG=∠GOB=![]() BOF
BOF
所以∠GOH=∠GOF﹣∠FOH
=![]() BOF﹣(∠AOH﹣∠AOF)
BOF﹣(∠AOH﹣∠AOF)
=![]() (180
(180![]() ﹣∠AOF)﹣
﹣∠AOF)﹣![]() AOE+∠AOF
AOE+∠AOF
=90![]() ﹣
﹣![]() AOF﹣
AOF﹣![]() (90
(90![]() +∠AOF)+∠AOF
+∠AOF)+∠AOF
=90![]() ﹣
﹣![]() AOF﹣45
AOF﹣45![]() ﹣
﹣![]() AOF+∠AOF
AOF+∠AOF
=45![]() ;
;
所以∠GOH的度数为45![]() ;
;
如图4,当OE落在其他位置时
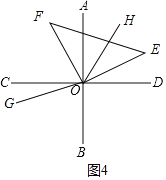
因为OH平分∠AOE
所以∠HOE=∠AOH=![]() AOE
AOE
因为OG平分∠BOF
∠FOG=∠GOB=![]() BOF
BOF
所以∠GOH=∠GOF+∠FOH
=![]() BOF+∠AOH+∠AOF
BOF+∠AOH+∠AOF
=![]() (180
(180![]() ﹣∠AOF)+
﹣∠AOF)+![]() AOE+∠AOF
AOE+∠AOF
=90![]() ﹣
﹣![]() AOF+
AOF+![]() (90
(90![]() ﹣∠AOF)+∠AOF
﹣∠AOF)+∠AOF
=90![]() ﹣
﹣![]() AOF+45
AOF+45![]() ﹣
﹣![]() AOF+∠AOF
AOF+∠AOF
=135![]() ;
;
所以∠GOH的度数为135![]() ;
;
综上所述:∠GOH的度数为45![]() 或135
或135![]() .
.


科目:初中数学 来源: 题型:
【题目】(1)某校举办秋季运动会,七(1)班和七(2)班进行拔河比赛,比赛规定标志物红绸向某班方向移动![]() 或
或![]() 以上,该班就获胜.红绸先向(2)班移动
以上,该班就获胜.红绸先向(2)班移动![]() ,后又向(1)班移动
,后又向(1)班移动![]() ,相持几秒后,红绸向(2)班移动
,相持几秒后,红绸向(2)班移动![]() ,随后又向(1)班移动
,随后又向(1)班移动![]() ,在一片欢呼声中,红绸再向(1)班移动
,在一片欢呼声中,红绸再向(1)班移动![]() ,裁判员一声哨响,比赛结束,请你用计算的方法说明最终获胜的是几班;
,裁判员一声哨响,比赛结束,请你用计算的方法说明最终获胜的是几班;
(2)已知![]() 、
、![]() 互为相反数,
互为相反数,![]() 、
、![]() 互为倒数,
互为倒数,![]() 的绝对值为2,求
的绝对值为2,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
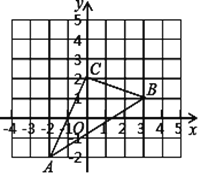
【题目】如图,△ABC在直角坐标系中,
(1)请写出![]() 各点的坐标;
各点的坐标;
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到![]() ,在图中画出三角形ABC变化后的位置,写出A′、B′、C′的坐标;
,在图中画出三角形ABC变化后的位置,写出A′、B′、C′的坐标;
(3)求出△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分别是BG,AC的中点.
(1)求证:DE=DF,DE⊥DF;
(2)连接EF,若AC=10,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
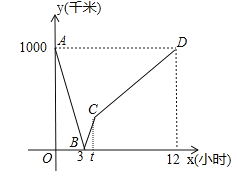
【题目】首条贯通丝绸之路经济带的高铁线﹣宝兰客专进入全线拉通试验阶段,宝兰客专的通车对加快西北地区与“一带一路”沿线国家和地区的经贸合作、人文交流具有十分重要的意义.试运行期间,一列动车从西安开往西宁,一列普通列车从西宁开往西安,两车同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示y与x之间的函数关系,根据图象进行一下探究:
【信息读取】
(1)西宁到西安两地相距 千米,两车出发后 小时相遇;
(2)普通列车到达终点共需 小时,普通列车的速度是 千米/小时.
【解决问题】
(3)求动车的速度;
(4)普通列车行驶t小时后,动车到达终点西宁,求此时普通列车还需行驶多少千米到达西安?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角△ABC中,∠A=60°,∠ACB=45°,以BC为弦作⊙O,交AC于点D,OD与BC交于点E,若AB与⊙O相切,则下列结论:
①∠BOD=90°;②DO∥AB;③CD=AD;④△BDE∽△BCD;⑤![]()
正确的有( )
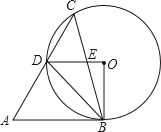
A. ①② B. ①④⑤ C. ①②④⑤ D. ①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中 AB=AC,D、E 两点分别在 AC、BC 上,BD 是∠ABC 的平分线,DE∥AB,若 BE=5cm,CE=3cm,则△CDE 的周长是( )
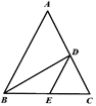
A. 13cmB. 11cmC. 9cmD. 8cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com