
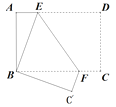
【题目】如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点![]() 处,折痕为EF,若∠ABE=20°,那么∠DEF的度数为_______.
处,折痕为EF,若∠ABE=20°,那么∠DEF的度数为_______.
【答案】55°
【解析】
由∠ABF、∠C′BF均与∠EBF互余,可知∠C′BF=∠ABF=20°;由折叠特性可知∠BC′F=90°可得出∠BFC′=70°;再根据2∠EFB+∠BFC′=180°可得出∠EFB=![]() =55°,结合平行线的性质求得∠DEF的度数.
=55°,结合平行线的性质求得∠DEF的度数.
解:∵四边形ABCD为长方形,
∴∠ABC=∠D=∠C=90°.
由折叠的特性可知:∠BC′F=∠C=90°,∠EBC′=∠D=90°.
∵∠ABE+∠EBF=90°,∠C′BF+∠EBF=90°,且∠ABE=20°,
∴∠C′BF=20°.
∵∠BC′F=90°,
∴∠BFC′=90°-∠C′BF=70°.
又∵2∠EFB+∠BFC′=180°,
∴∠EFB=![]() =55°
=55°
∵AD∥BC,
∴∠DEF=∠EFB=55°.
故答案为:55°.


科目:初中数学 来源: 题型:
【题目】如图,DB∥AC,且DB=![]() AC,E是AC的中点,
AC,E是AC的中点,
(1)求证:BC=DE;
(2)连接AD、BE,若要使四边形DBEA是矩形,则给△ABC添加什么条件,为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2m+3的正方形纸片中剪出一个边长为m+3的正方形之后,剩余部分可剪拼成一个长方形,

(1)求拼接成的长方形面积.
(2)若拼成的长方形一边长为 m,求此长方形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
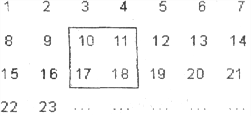
【题目】把正整数1,2,3,4,……,2009排列成如图所示的一个表
(1)用一正方形在表中随意框住4个数,把其中最小的数记为x,另三个数用含x的式子表示出来,从小到大依次是 , , 。
(2)当被框住的4个数之和等于416时,x的值是多少?
(3)被框住的4个数之和能否等于622?如果能,请求出此时x的值;如果不能,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线AB与CD相交于点O,且∠AOD=90°,现将一个直角三角尺的直角顶点放在点O处,把该直角三角尺OEF绕着点O旋转,作射线OH平分∠AOE.
(1)如图1所示,当∠DOE=20°时,∠FOH的度数是 .
(2)若将直角三角尺OEF绕点O旋转至图2的位置,试判断∠FOH和∠BOE之间的数量关系,并说明理由.
(3)若再作射线OG平分∠BOF,试求∠GOH的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将在Rt△ABC绕其锐角顶点A旋转90°得到在Rt△ADE,连接BE,延长DE、BC相交于点F,则有∠BFE=90°,且四边形ACFD是一个正方形.
(1)判断△ABE的形状,并证明你的结论;
(2)用含b代数式表示四边形ABFE的面积;
(3)求证:a2+b2=c2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,AB=6cm,BC=8cm,对角线AC,BD交于点0.点P从点A出发,沿方向匀速运动,速度为1cm/s;同时,点Q从点D出发,沿DC方向匀速运动,速度为1cm/s;当一个点停止运动时,另一个点也停止运动.连接PO并延长,交BC于点E,过点Q作QF∥AC,交BD于点F.设运动时间为t(s)(0<t<6),解答下列问题:
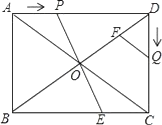
(1)当t为何值时,△AOP是等腰三角形?
(2)设五边形OECQF的面积为S(cm2),试确定S与t的函数关系式;
(3)在运动过程中,是否存在某一时刻t,使S五边形S五边形OECQF:S△ACD=9:16?若存在,求出t的值;若不存在,请说明理由;
(4)在运动过程中,是否存在某一时刻t,使OD平分∠COP?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com