
【题目】已知:如图,在矩形ABCD中,AB=6cm,BC=8cm,对角线AC,BD交于点0.点P从点A出发,沿方向匀速运动,速度为1cm/s;同时,点Q从点D出发,沿DC方向匀速运动,速度为1cm/s;当一个点停止运动时,另一个点也停止运动.连接PO并延长,交BC于点E,过点Q作QF∥AC,交BD于点F.设运动时间为t(s)(0<t<6),解答下列问题:
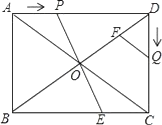
(1)当t为何值时,△AOP是等腰三角形?
(2)设五边形OECQF的面积为S(cm2),试确定S与t的函数关系式;
(3)在运动过程中,是否存在某一时刻t,使S五边形S五边形OECQF:S△ACD=9:16?若存在,求出t的值;若不存在,请说明理由;
(4)在运动过程中,是否存在某一时刻t,使OD平分∠COP?若存在,求出t的值;若不存在,请说明理由.
【答案】(1)![]() 或5;(2)
或5;(2)![]() ;(3)
;(3)![]() ;(4)2.88.
;(4)2.88.
【解析】试题(1)根据矩形的性质和勾股定理得到AC=10,①当AP=PO=t,如图1,过P作PM⊥AO,根据相似三角形的性质得到AP=t=![]() ,②当AP=AO=t=5,于是得到结论;
,②当AP=AO=t=5,于是得到结论;
(2)作EH⊥AC于H,QM⊥AC于M,DN⊥AC于N,交QF于G,根据全等三角形的性质得到CE=AP=t,根据相似三角形的性质表示出EH,根据相似三角形的性质表示出QM,FQ,根据图形的面积即可得到结论;
(3)根据题意列方程得到t的值,于是得到结论;
(4)由角平分线的性质得到DM的长,根据勾股定理得到ON的长,由三角形的面积公式表示出OP,根据勾股定理列方程即可得到结论.
试题解析:(1)∵在矩形ABCD中,Ab=6cm,BC=8cm,
∴AC=10,
①当AP=PO=t,如图1,过P作PM⊥AO,
∴AM=![]() AO=
AO=![]() ,
,
∵∠PMA=∠ADC=90°,∠PAM=∠CAD,
∴△APM∽△ADC,
∴![]() ,
,
∴AP=t=![]() ,
,
②当AP=AO=t=5,
∴当t为![]() 或5时,△AOP是等腰三角形;
或5时,△AOP是等腰三角形;
(2)作EH⊥AC于H,QM⊥AC于M,DN⊥AC于N,交QF于G,在△APO与△CEO中,
∵∠PAO=∠ECO,AO=OC,∠AOP=∠COE,
∴△AOP≌△COE,
∴CE=AP=t,
∵△CEH∽△ABC,
∴![]() ,
,
∴EH=![]() ,
,
∵DN=![]() =
=![]() ,
,
∵QM∥DN,
∴△CQM∽△CDN,
∴![]() ,即
,即![]() ,
,
∴QM=![]() ,
,
∴DG=![]() =
=![]() ,
,
∵FQ∥AC,
∴△DFQ∽△DOC,
∴![]() ,
,
∴FQ=![]() ,
,
∴S五边形OECQF=S△OEC+S四边形OCQF=![]() =
=![]() ,
,
∴S与t的函数关系式为![]() ;
;
(3)存在,
∵S△ACD=![]() ×6×8=24,
×6×8=24,
∴S五边形OECQF:S△ACD=(![]() ):24=9:16,解得t=
):24=9:16,解得t=![]() ,t=0,(不合题意,舍去),
,t=0,(不合题意,舍去),
∴t=![]() 时,S五边形S五边形OECQF:S△ACD=9:16;
时,S五边形S五边形OECQF:S△ACD=9:16;
(4)如图3,过D作DM⊥AC于M,DN⊥AC于N,
∵∠POD=∠COD,
∴DM=DN=![]() ,
,
∴ON=OM=![]() =
=![]() ,
,
∵OPDM=3PD,
∴OP=![]() ,
,
∴PM=![]() ,
,
∵![]() ,
,
∴![]() ,解得:t≈15(不合题意,舍去),t≈2.88,
,解得:t≈15(不合题意,舍去),t≈2.88,
∴当t=2.88时,OD平分∠COP.



科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中 AB=AC,D、E 两点分别在 AC、BC 上,BD 是∠ABC 的平分线,DE∥AB,若 BE=5cm,CE=3cm,则△CDE 的周长是( )
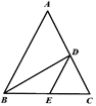
A. 13cmB. 11cmC. 9cmD. 8cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我国民间流传着许多诗歌形式的数学算题,这些题目叙述生动、活泼,它们大都是关于方程和方程组的应用题.由于诗歌的语言通俗易懂、雅俗共赏,因而一扫纯数学的枯燥无味之感,令人耳目一新,回味无穷.请根据下列诗意列方程组解应用题.
周瑜寿属:而立之年督东吴,早逝英年两位数;十比个位正小三,个位六倍与寿符;哪位同学算得快,多少年寿属周瑜?诗的意思是:周瑜病逝时的年龄是一个大于30的两位数,其十位上的数字比个位数字小3,个位上的数字的6倍正好等于这个两位数,求这个两位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若等腰三角形的顶角为36°,则这个三角形就是黄金三角形。如图,在△ABC中,BA=BC,D 在边 CB 上,且 DB=DA=AC。
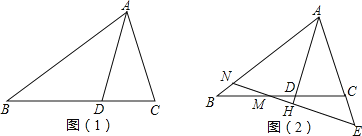
(1)如图1,写出图中所有的黄金三角形,并证明;
(2)若 M为线段 BC上的点,过 M作直线MH⊥AD于 H,分别交直线 AB,AC与点N,E,如图 2,试写出线段 BN、CE、CD之间的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人共同计算一道整式乘法题:(2x+a)(3x+b).甲由于把第一个多项式中的“+a”看成了“﹣a”,得到的结果为6x2+11x﹣10;乙由于漏抄了第二个多项式中x的系数,得到的结果为2x2﹣9x+10.
(1)求a、b的值.
(2)计算这道乘法题的正确结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,F是CD上一点,E是BF上一点,连接AE、AC、DE.若AB=AC,AD=AE,∠BAC=∠DAE=70°,AE平分∠BAC,则下列结论中:①△ABE≌△ACD:②BE=EF;③∠BFD=110°;④AC垂直平分DE,正确的个数有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、E、C、F在同一直线上,且AB=DE,AC=DF,BE=CF,请将下面说明ΔABC≌ΔDEF的过程和理由补充完整。
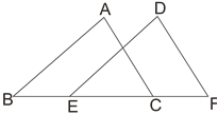
解:∵BE=CF ( )
∴BE+EC=CF+EC
即BC=EF
在ΔABC和ΔDEF中
AB= ( )
=DF( )
BC=
∴ΔABC≌ΔDEF ( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com