
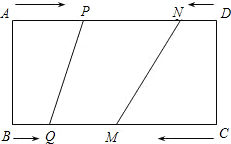
 ��ͼ��ʾ���ڳ�����ABCD�У�BC=24cm��AB=10cm����P��Q��M��N�ֱ��A��B��C��D������AD��BC��CB��DA�����ڳ����εı���ͬʱ�˶�������һ�����ȵ��������˶��ߵ���һ���˵�ʱ���˶���ֹͣ����֪����ͬʱ���ڣ���BQ=xcm��x��0������AP=2xcm��CM=3xcm��DN=x2cm��
��ͼ��ʾ���ڳ�����ABCD�У�BC=24cm��AB=10cm����P��Q��M��N�ֱ��A��B��C��D������AD��BC��CB��DA�����ڳ����εı���ͬʱ�˶�������һ�����ȵ��������˶��ߵ���һ���˵�ʱ���˶���ֹͣ����֪����ͬʱ���ڣ���BQ=xcm��x��0������AP=2xcm��CM=3xcm��DN=x2cm������ ��1���ֱ���BQ=x=24��AP=2x=24��CM=3x=24��DN=x2=24�������Ӧ��x��ֵ��ȡx����С��ֵ��Ȼ��ֱ����AP��BQ��CM��QM��ֵ��Ȼ��������ε������ʽ���㼴�ɣ�
��2����PQ��MNΪ���ߣ��Ծ��εıߣ�AD��BC����һ����Ϊ�����߹���һ�������εı��������ǵ�P��N�غ��ҵ�Q��M���غϣ���ʱAP+ND=AD��2x+x2=24cm��BQ+MC��BC��x+3x��24cm�����ߵ�Q��M�غ��ҵ�P��N���غϣ���ʱAP+ND��AD��2x+x2��24cm��BQ+MC=BC��x+3x=24cm�����Կ��Ը�����������������x��ֵ��
��3����P��Q��M��NΪ������ı�����ƽ���ı��εĻ�����Ϊ�ɵ�һ�ʿ�֪��Qֻ���ڵ�M����࣮����P�ڵ�N�����ʱ��AP=MC��BQ=ND������P�ڵ�N���Ҳ�ʱ��AN=MC��BQ=PD�����Կ��Ը�����Щ�����г����̹�ϵʽ��
��� �⣺��1����BQ=x=24����ã�x=24��
��AP=2x=24����ã�x=12��
��CM=3x=24�����x=8��
��DN=x2=24����ã�x=2$\sqrt{6}$��
��2$\sqrt{6}$��8��12��24��
�൱x=2$\sqrt{6}$cm������N����A�㣩ʱ����P��Q��M��Nֹͣ�˶���
��x=2$\sqrt{6}$cmʱ��AP=4$\sqrt{6}$cm��CM=6$\sqrt{6}$cm��BQ=2$\sqrt{6}$cm��
��QM=BC-BQ-CM=24-8$\sqrt{6}$��
��ͼ1��ʾ��
������NQMP�����=$\frac{1}{2}$��NP+QM����AB=$\frac{1}{2}$����4$\sqrt{6}$+24-8$\sqrt{6}$����10=120-20$\sqrt{6}$cm��
��2������P���N�غϻ��Q���M�غ�ʱ����PQ��MNΪ���ߣ��Ծ��εıߣ�AD��BC����һ����Ϊ�����߿��ܹ���һ�������Σ�
�ٵ���P���N�غ�ʱ����ͼ2��ʾ��
��x2+2x=24����x1=4��x2=-6����ȥ����
��ΪBQ+CM=x+3x=16��24����ʱ��Q���M���غϣ�
����x=4�������⣮
�ڵ���Q���M�غ�ʱ����x+3x=24����x=6��
��ʱDN=x2=36��24�����������⣮
�ʵ�Q���M�����غϣ�
���Ե�xΪ4ʱ����PQ��MNΪ���ߣ��Ծ��εıߣ�AD��BC����һ����Ϊ�����߹���һ�������Σ�
��3���ɣ�2��֪����Qֻ���ڵ�M����࣬
�ٵ���P�ڵ�N�����ʱ��
��24-��x+3x��=24-��2x+x2����
���x1=0����ȥ����x2=2��
��x=2ʱ�ı���PQMN��ƽ���ı��Σ�
�ڵ���P�ڵ�N���Ҳ�ʱ��
��24-��x+3x��=��2x+x2��-24��
���x1=-3-$\sqrt{57}$����ȥ����x2=-3+$\sqrt{57}$��
��x=-3+$\sqrt{57}$ʱ�ı���NQMP��ƽ���ı��Σ�
���Ե�x=2��x=-3+$\sqrt{57}$ʱ����P��Q��M��NΪ������ı�����ƽ���ı��Σ�
���� ������һ���˶������⣬���˶���ƽ���ı��ε����ʽ��������������Ŀ�ĵ�����ϵ�г�һԪ���η��̽�����⣮����ʱ����Ҫ�����Ķ���Ŀ����ȷ�������⣬Ȼ�������ȷ��δ֪���г����̽��⣬������������˼�룮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �����г������̵�������� | |
| B�� | ��������ɻ����ÿ��Ƿ�Я����Σ����Ʒ | |
| C�� | ����ijƷ���չ�ƹܵ�ʹ������ | |
| D�� | ���顶������ի����Ŀ����������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
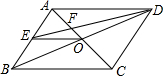 ��ͼ��OΪ?ABCD�ĶԽ��߽��㣬EΪAB���е㣬DE��AC�ڵ�F����S��ABCD=16����S��DOE��ֵΪ2��
��ͼ��OΪ?ABCD�ĶԽ��߽��㣬EΪAB���е㣬DE��AC�ڵ�F����S��ABCD=16����S��DOE��ֵΪ2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
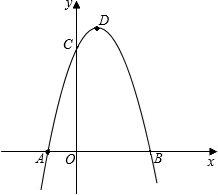 ��ͼ��������y=-x2+2x+3��x���ཻ��A��B���㣨��A�ڵ�B����ࣩ����y���ཻ�ڵ�C������ΪD��
��ͼ��������y=-x2+2x+3��x���ཻ��A��B���㣨��A�ڵ�B����ࣩ����y���ཻ�ڵ�C������ΪD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{80}{x}$-$\frac{80}{3x}$=40 | B�� | $\frac{80}{x}$-$\frac{80}{3x}$=2.4 | C�� | $\frac{80}{x}$-2=$\frac{80}{3x}$+$\frac{2}{3}$ | D�� | $\frac{80}{x}$+2=$\frac{80}{3x}$-$\frac{2}{3}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com