
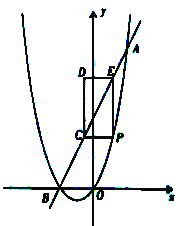
【题目】(2016贵州省毕节市第27题)如图,已知抛物线![]() 与直线
与直线![]() 交于A(a,8)、B两点,点P是抛物线上A、B之间的一个动点,过点P分别作
交于A(a,8)、B两点,点P是抛物线上A、B之间的一个动点,过点P分别作![]() 轴、
轴、![]() 轴的平行线与直线AB交于点C和点E.
轴的平行线与直线AB交于点C和点E.
(1)求抛物线的解析式;
(2)若C 为AB中点,求PC的长;
(3)如图,以PC,PE为边构造矩形PCDE,设点D的坐标为(m,n),请求出m,n之间的关系式。
【答案】(1)、y=![]() +2x;(2)、
+2x;(2)、![]() -1;(3)、
-1;(3)、![]() -4n-8m-16=0
-4n-8m-16=0
【解析】
试题分析:(1)、首先根据点A在一次函数上求出点A的坐标,然后代入二次函数得出解析式;(2)、根据一次函数和二次函数得出点B的坐标,根据中点的性质得出点C的坐标,根据点P在抛物线上得出点P的坐标,从而得出PC的长度;(3)、根据点D的坐标从而得出点C、点E和点P的坐标,根据DE=CP得出m和n之间的关系式.
试题解析:(1)、∵A(a,8)在直线上 ∴8=2a+4 解得:a=2
将A(2,8)代入二次函数可得:8=4+2b 解得:b=2 ∴抛物线的解析式为:y=![]() +2x
+2x
(2)、由 可得点B的坐标为(-2,0) 根据中点坐标公式可得:C(0,4)
可得点B的坐标为(-2,0) 根据中点坐标公式可得:C(0,4)
∵点P在抛物线上且纵坐标与C相同 ∴P(![]() -1,4) ∴PC=
-1,4) ∴PC=![]() -1-0=
-1-0=![]() -1.
-1.
(3)、∵D(m,n) ∴C(m,2m+4),E(![]() ,n),P(
,n),P(![]() ,2m+4)
,2m+4)
由DE=CP可得:![]() -m=
-m=![]() -m 化简得:
-m 化简得:![]() -4n-8m-16=0
-4n-8m-16=0


科目:初中数学 来源: 题型:
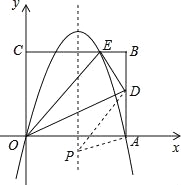
【题目】(2016广西省贺州市第26题)如图,矩形的边OA在x轴上,边OC在y轴上,点B的坐标为(10,8),沿直线OD折叠矩形,使点A正好落在BC上的E处,E点坐标为(6,8),抛物线y=ax2+bx+c经过O、A、E三点.
(1)求此抛物线的解析式;
(2)求AD的长;
(3)点P是抛物线对称轴上的一动点,当△PAD的周长最小时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
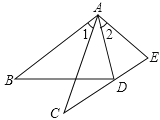
【题目】在数学课上,林老师在黑板上画出如图所示的△ABD和△ACE两个三角形,并写出四个条件:①AB=AC;②AD=AE;③∠1=∠2;④∠B=∠C.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.
题设:___________;结论:_______.(均填写序号)
证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
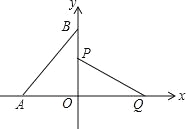
【题目】(2016浙江省舟山市第16题)如图,在直角坐标系中,点A,B分别在x轴,y轴上,点A的坐标为(﹣1,0),∠ABO=30°,线段PQ的端点P从点O出发,沿△OBA的边按O→B→A→O运动一周,同时另一端点Q随之在x轴的非负半轴上运动,如果PQ=![]() ,那么当点P运动一周时,点Q运动的总路程为 .
,那么当点P运动一周时,点Q运动的总路程为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=3x2向左平移1个单位,再向下平移2个单位,所得到的抛物线是 ( )
A. y=3(x-1)2-2 B. y=3(x+1)2-2
C. y=3(x+1)2+2 D. y=3(x-1)2+2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com