17.先阅读下列解答过程,再解答.
形如$\sqrt{m±2\sqrt{n}}$的化简,只要我们找到两个数a,b,使a+b=m,ab=n,
即($\sqrt{a}$)2+($\sqrt{b}$)2=m,$\sqrt{a}$-$\sqrt{b}$=$\sqrt{n}$,那么便有:
$\sqrt{m±2\sqrt{n}}$=$\sqrt{(\sqrt{a}±\sqrt{b})^{2}}$=$\sqrt{a}$±$\sqrt{b}$(a>b).
例如:化简:$\sqrt{7+4\sqrt{3}}$.
解:首先把$\sqrt{7+4\sqrt{3}}$化为$\sqrt{7+2\sqrt{12}}$,这里m=7,n=12,
由于4+3=7,4×3=12,
即($\sqrt{4}$)2+($\sqrt{3}$)2=7,$\sqrt{4}$×$\sqrt{3}$=$\sqrt{12}$,
所以$\sqrt{7+4\sqrt{3}}$=$\sqrt{7+2\sqrt{12}}$=$\sqrt{(\sqrt{4}+\sqrt{3})^{2}}$=2+$\sqrt{3}$.
根据上述例题的方法化简:$\sqrt{13-2\sqrt{42}}$.
分析 首先确定m=13,n=42,然后确定两个数的和是13,积是42,然后根据例题即可解答.
解答 解:∵m=13,n=42,
又∵6+7=13,6×7=42,
即($\sqrt{6}$)2=6,($\sqrt{7}$)2=7,$\sqrt{6}$×$\sqrt{7}$=$\sqrt{42}$,
∴$\sqrt{13-2\sqrt{42}}$=$\sqrt{(\sqrt{6}-\sqrt{7})^{2}}$=$\sqrt{7}$-$\sqrt{6}$.
点评 本题考查了二次根式的化简,正确读懂例题是本题的关键.


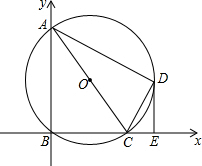 如图,在平面直角坐标系中,点A、C的坐标分别为(0,8)、(6,0),以AC为直径作⊙O,交坐标轴于点B,点D是⊙O 上一点,且弧BD=弧AD,过点D作DE⊥BC,垂足为E.
如图,在平面直角坐标系中,点A、C的坐标分别为(0,8)、(6,0),以AC为直径作⊙O,交坐标轴于点B,点D是⊙O 上一点,且弧BD=弧AD,过点D作DE⊥BC,垂足为E.