
分析 先分母因式分解,再通分计算,再计算加减法,约分计算即可求解.
解答 解:$\frac{b-c}{{a}^{2}-ab-ac+bc}$-$\frac{c-a}{{b}^{2}-bc-ab+ac}$+$\frac{a-b}{{c}^{2}-ac-bc+ab}$
=$\frac{b-c}{(a-b)(a-c)}$-$\frac{a-c}{(a-b)(b-c)}$+$\frac{a-b}{(b-c)(a-c)}$
=$\frac{-2(a-b)(b-c)}{(a-b)(a-c)(b-c)}$
=-$\frac{2}{a-c}$.
点评 考查了分式的加减法,说明:①分式的通分必须注意整个分子和整个分母,分母是多项式时,必须先分解因式,分子是多项式时,要把分母所乘的相同式子与这个多项式相乘,而不能只同其中某一项相乘.②通分是和约分是相反的一种变换.约分是把分子和分母的所有公因式约去,将分式化为较简单的形式;通分是分别把每一个分式的分子分母同乘以相同的因式,使几个较简单的分式变成分母相同的较复杂的形式.约分是对一个分式而言的;通分则是对两个或两个以上的分式来说的.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:解答题
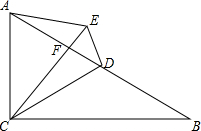 如图,在△ABC中,∠ACB=90°,∠B=30°,且点D是AB的中点,E为△ABC外一点,连接AE、DE,连接CE交AB于F,且∠CAD=∠CED.
如图,在△ABC中,∠ACB=90°,∠B=30°,且点D是AB的中点,E为△ABC外一点,连接AE、DE,连接CE交AB于F,且∠CAD=∠CED.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,菱形ABCD的对角线长分别为a、b.它的面积为S,以菱形ABCD各边中点为顶点作四边形A1B1C1D1,它的面积为S1,然后再以四边形A1B1C1D1的中点为顶点作四边形如此下去,得到四边形A2B2C2D2,它的面积为S2,如此下去,得到四边形AnBnCnDn,
如图,菱形ABCD的对角线长分别为a、b.它的面积为S,以菱形ABCD各边中点为顶点作四边形A1B1C1D1,它的面积为S1,然后再以四边形A1B1C1D1的中点为顶点作四边形如此下去,得到四边形A2B2C2D2,它的面积为S2,如此下去,得到四边形AnBnCnDn,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知直线AB∥DE.
如图,已知直线AB∥DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com