
 ��ͼ������ABCD�ĶԽ��߳��ֱ�Ϊa��b���������ΪS��������ABCD�����е�Ϊ�������ı���A1B1C1D1���������ΪS1��Ȼ�������ı���A1B1C1D1���е�Ϊ�������ı��������ȥ���õ��ı���A2B2C2D2���������ΪS2�������ȥ���õ��ı���AnBnCnDn��
��ͼ������ABCD�ĶԽ��߳��ֱ�Ϊa��b���������ΪS��������ABCD�����е�Ϊ�������ı���A1B1C1D1���������ΪS1��Ȼ�������ı���A1B1C1D1���е�Ϊ�������ı��������ȥ���õ��ı���A2B2C2D2���������ΪS2�������ȥ���õ��ı���AnBnCnDn������ ��1���������ABCD�����Ϊ$\frac{1}{2}$ab�����S��ABD=S��CBD=S��ADC=S��ABC=$\frac{1}{4}$ab���������������ε����ʷֱ����S${\;}_{��D{D}_{1}{C}_{1}}$=S${\;}_{A{A}_{1}{D}_{1}}$=S${\;}_{B{B}_{1}{A}_{1}}$=S${\;}_{C{C}_{1}{B}_{1}}$=$\frac{1}{16}$ab�����ε������ȥ�ĸ������ε��������������𰸣�
��2�����ݣ�1��������Ľ���ó����ɣ���������𰸣�
��3�����ݣ�1��������Ľ���ó����ɣ���������𰸣�
��� �⣺��1��������ABCD�ĶԽ��߳��ֱ�Ϊa��b��
������ABCD�����Ϊ$\frac{1}{2}$ab��
��S��ABD=S��CBD=S��ADC=S��ABC=$\frac{1}{2}$S����ABCD=$\frac{1}{4}$ab��
��D1��C1�ֱ�ΪAD��DC���е㣬
��D1C1=$\frac{1}{2}$AC=$\frac{1}{2}$a��D1C1��AC��
���DD1C1�ס�DAC��
��$\frac{{S}_{��DD{{\;}_{1}C}_{1}}}{{S}_{��DAC}}$=��$\frac{{D}_{1}{C}_{1}}{AC}$��2=$\frac{1}{4}$��
��S${\;}_{��D{D}_{1}{C}_{1}}$=$\frac{1}{4}$S��DAC=$\frac{1}{16}$ab��
ͬ��S${\;}_{A{A}_{1}{D}_{1}}$=$\frac{1}{16}$ab��S${\;}_{B{B}_{1}{A}_{1}}$=$\frac{1}{16}$ab��S${\;}_{C{C}_{1}{B}_{1}}$=$\frac{1}{16}$ab��
��S1=$\frac{1}{2}$ab-4��$\frac{1}{16}$ab=$\frac{1}{4}$ab��
ͬ��S2=$\frac{1}{8}$ab��
��2�����ɣ�1��֪��S1=$\frac{1}{4}$ab��S2=$\frac{1}{8}$ab��S3=$\frac{1}{16}$ab��
��ͬ���ı���A4B4C4D4�������$\frac{1}{32}$ab��
��3�����ɣ�1��֪��S1=$\frac{1}{4}$ab��S2=$\frac{1}{8}$ab��S3=$\frac{1}{16}$ab��
���ı���AnBnCnD�������$\frac{1}{{2}^{n+1}}$ab��
���� ���⿼�������ε����ʣ����������ε����ʺ��ж���Ӧ�ã��ܸ�������Ľ���ó������ǽ����Ĺؼ���


 ��Ȥ����¹�֪��ϵ�д�
��Ȥ����¹�֪��ϵ�д� Ӣ��СӢ������Ĭдϵ�д�
Ӣ��СӢ������Ĭдϵ�д� �����ҵ���������ͯ������ϵ�д�
�����ҵ���������ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
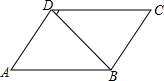 ��֪��ƽ���ı���ABCD��BDΪ�Խ��ߣ���ͼ����A=70�㣬��BDC=30�㣬AD=15����C����ADB�Ķ���������BC�ߵij���
��֪��ƽ���ı���ABCD��BDΪ�Խ��ߣ���ͼ����A=70�㣬��BDC=30�㣬AD=15����C����ADB�Ķ���������BC�ߵij����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
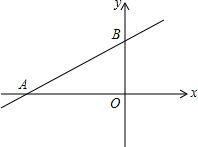 һ�κ���y=$\frac{\sqrt{3}}{3}$x+3��ͼ��ֱ�x��y����A��B���㣬�Ƿ����������ϴ���һ��Cʹ�á�ABCΪֱ�������Σ����У������C������꣮
һ�κ���y=$\frac{\sqrt{3}}{3}$x+3��ͼ��ֱ�x��y����A��B���㣬�Ƿ����������ϴ���һ��Cʹ�á�ABCΪֱ�������Σ����У������C������꣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com