
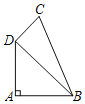
【题目】如图,在四边形ABCD中,已知AB=AD=2,BC=3,CD=1,∠A=90°.
(1)求BD的长;
(2)求∠ADC的度数.
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AB=AC,D是△ABC外接圆劣弧AC上的点(不与A,C重合),延长BD至E.
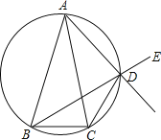
(1)求证:AD的延长线平分∠CDE;
(2)若∠BAC=30°,且△ABC底边BC边上高为1,求△ABC外接圆的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
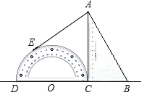
【题目】如图,将量角器和含![]() 角的一块直角三角板紧靠着放在同一平面内,使
角的一块直角三角板紧靠着放在同一平面内,使![]() ,
,![]() ,
,![]() 在一条直线上,且
在一条直线上,且![]() ,过点
,过点![]() 作量角器圆弧所在圆的切线,切点为
作量角器圆弧所在圆的切线,切点为![]() ,如果
,如果![]() ,则
,则![]() 的长是________
的长是________![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017甘肃省天水市)△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合,将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.
(1)如图①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE;
(2)如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;并求当BP=2,CQ=9时BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
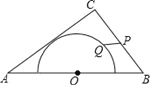
【题目】如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最小值是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车4S店销售某种型号的汽车,每辆进货价为15万元,该店经过一段时间的市场调研发现:当销售价为25万元时,平均每周能售出8辆,而当销售价每降低0.5万元时,平均每周能多售出1辆.该4S店要想平均每周的销售利润为90万元,并且使成本尽可能的低,则每辆汽车的定价应为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图4所示的是桥梁的两条钢缆具有相同的抛物线形状.按照图中建立的直角坐标系,右面的一条抛物线的解析式为y=x2-4x+5表示,而且左右两条抛物线关于y轴对称,则左面钢缆的表达式为_________________________________.
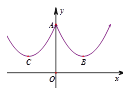
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据图①所示的程序,得到了如图②y与x的函数图像,若点M是y轴正半轴上任意一点,过点M作PQ∥x轴交图像于点P、Q,连接OP、OQ.则以下结论:
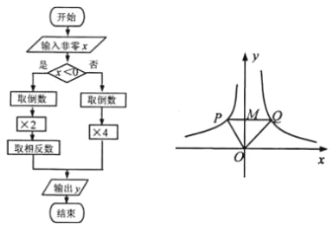
①x<0时,y=![]() ; ②△OPQ的面积为定值; ③x>0时,y随x的增大而增大;
; ②△OPQ的面积为定值; ③x>0时,y随x的增大而增大;
④MQ=2PM; ⑤∠POQ可以等于90°.
其中正确结论序号是
A. ①②③ B. ②③④ C. ③④⑤ D. ②④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com