
【题目】用适当的方法解方程
(1)x2-4x+1=0
(2)(2x+1)2=3(2x+1)
(3)(x+3)(x-6)=-8
(4)2x2-x-15=0
【答案】(1)x1=2+![]() ,x2=2-
,x2=2-![]() ;(2)x =
;(2)x =![]() ,x =1;(3)x1=5,x2=-2;(4)x =3,x =
,x =1;(3)x1=5,x2=-2;(4)x =3,x =![]() .
.
【解析】
(1)用配方法解一元二次方程; (2)用因公式分解法解一元二次方程;(3)用十字相乘法解一元二次方程(4)用十字相乘法解一元二次方程.
(1)x2-4x+1=0
(x-2)2=3,
则 x-2=±![]() ,
,
解得:x1=2+![]() ,x2=2-
,x2=2-![]() ;
;
(2)(2x+1)2=3(2x+1)
(2x+1)(2x+1-3)=0,
解得:x =![]() ,x =1;
,x =1;
(3)(x+3)(x-6)=-8
x2-6x+3x-18=-8,
则 x2-3x-10=0,
(x-5)(x+2)=0,
解得:x1=5,x2=-2;
(4)2x2-x-15=0
(x-3)(2x+5)=0,
解得:x =3,x =![]() .
.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:
①∠EBG=45°; ②△DEF∽△ABG;
③S△ABG=S△FGH; ④AG+DF=FG.
其中正确的是_____.(填写正确结论的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
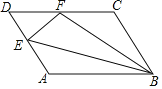
【题目】如图,在平行四边形ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD上的点F处,若△FDE的周长为12,△FCB的周长为28,则FC的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高科技发展公司投资500万元,成功研制出一种市场需求量较大的高科技替代产品,并投入资金1500万元作为固定投资,已知生产每件产品的成本是40元.在销售过程中发现:当销售单价定为100元时,年销售量为20万件;销售单价每增加10元,年销售量将减少1万件,设销售单价为x(元),年销售量为y(万件),年获利(年获利=年销售额一生产成本—投资)为z(万元).
(1)试写出y与x之间的函数关系式(不写x的取值范围);
(2)试写出z与x之间的函数关系式(不写x的取值范围);
(3)公司计划,在第一年按年获利最大确定销售单价进行销售;到第二年年底获利不低于1130万元,请借助函数的大致图象说明:第二年的销售单价x(元)应确定在什么范围内?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个正方体的六个面上分别标有数字 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
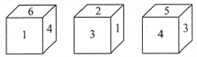
, ![]() ,从三个不同的角度观察这个正方体所得到的结果如图所示,如果标有数字
,从三个不同的角度观察这个正方体所得到的结果如图所示,如果标有数字 ![]() 的面所对面上的数字记为
的面所对面上的数字记为 ![]() ,
, ![]() 的面所对面上数字记为
的面所对面上数字记为 ![]() ,那么
,那么 ![]() 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC中,∠C=90°,AC=6,BC=8,D是AB的中点,E、F分别是AC、BC上两点,且ED⊥FD.
(1)如图1,若E是AC中点,则BF=______,EF=______,AE2+BF2______EF2(填“>,<或=”);
(2)如图2,若点E是AC边上任意一点,AE2+BF2_____EF2(填“>,<或=”),请说明理由;
(3)若点E在CA延长上,(2)中三条线段之间的关系是否成立?请画图说明.



查看答案和解析>>
科目:初中数学 来源: 题型:
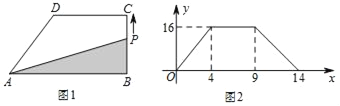
【题目】如图1,在直角梯形ABCD中,动点P从B点出发,沿B→C→D→A匀速运动,设点P运动的路程为x,△ABP的面积为y,图象如图2所示.
(1)在这个变化中,自变量、因变量分别是 、 ;
(2)当点P运动的路程x=4时,△ABP的面积为y= ;
(3)求AB的长和梯形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
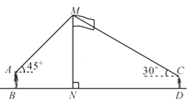
【题目】如图,某数学兴趣小组在活动课上测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7 m,看旗杆顶部M的仰角为45°;小红的眼睛与地面的距离(CD)是1.5 m,看旗杆顶部M的仰角为30°.两人相距30米且位于旗杆两侧(点B,N,D在同一条直线上).求旗杆MN的高度.(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732,结果保留整数)
≈1.732,结果保留整数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com