
【题目】Rt△ABC中,∠C=90°,AC=6,BC=8,D是AB的中点,E、F分别是AC、BC上两点,且ED⊥FD.
(1)如图1,若E是AC中点,则BF=______,EF=______,AE2+BF2______EF2(填“>,<或=”);
(2)如图2,若点E是AC边上任意一点,AE2+BF2_____EF2(填“>,<或=”),请说明理由;
(3)若点E在CA延长上,(2)中三条线段之间的关系是否成立?请画图说明.



【答案】(1)4;5;=;(2)=;证明见解析;(3)见解析.
【解析】
(1)由∠C=90°,AC=6,BC=8,可得![]() ,
,
又因为E是AC的中点,D是AB的中点,可得![]() ,所以∠DEF=∠CFE,因为ED⊥FD,所以∠EDF=90°,即∠CEF+∠CFE=∠DFE+∠DEF=90°,推出∠DFE=∠CEF,得到DF∥AC,又因为D为AB中点,推出F是BC的中点,所以
,所以∠DEF=∠CFE,因为ED⊥FD,所以∠EDF=90°,即∠CEF+∠CFE=∠DFE+∠DEF=90°,推出∠DFE=∠CEF,得到DF∥AC,又因为D为AB中点,推出F是BC的中点,所以![]() ,因为E是AC的中点,F为BC中点,所以
,因为E是AC的中点,F为BC中点,所以![]() ,由勾股定理得
,由勾股定理得![]() ,等量替代即可得到
,等量替代即可得到![]() ;
;
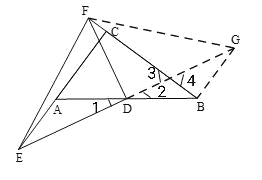
(2)如图,延长ED至G使得ED =DG,连接BG,FG,因为D是AB的中点,可得AD=BD,通过证△ADE≌△BDG,可得AE=BG,∠A=∠3,又∠C =90°,所以∠A+∠ABC=90°,所以∠3+∠ABC=∠FBG=90°,可得BG2+BF2=FG2,因为AE=BG,所以AE2+BF2=FG2,因为DE=DG,∠EDF=90°,所以FE=FG,即可推出AE2+BF2=EF2;
(3)成立,延长ED至G使得ED=DG,连接BG,FG,因为D是AB的中点,可得AD=BD,因为∠1=∠2,DE=DG,得到△ADE≌△BDG,所以AE=BG,∠AED=∠BGD,因为∠3=∠4,∠AED=∠BGD,推出∠GBF=∠C=90°,因为FD⊥ED,D为EG中点,所以EF=FG,又在Rt△BFG中,BG2+BF2=FG2,等量替代可得AE2+BF2=EF2;
解:(1)∵∠C=90°,AC=6,BC=8,
∴![]() ,
,
∵E是AC的中点,D是AB的中点,
∴![]() ,
,
∴∠DEF=∠CFE,
∵ED⊥FD,
∴∠EDF=90°,
∴∠CEF+∠CFE=∠DFE+∠DEF=90°,
∴∠DFE=∠CEF,
∴DF∥AC,
∵D为AB中点,
∴F为BC中点,
∴![]() ,
,
∵E是AC的中点,F为BC中点,
∴![]() ,
,
∵![]() ,
,
∴![]() ;
;
故答案为:4; 5;AE2+BF2=EF2;
(2)AE2+BF2=EF2,
如图,延长ED至G使得ED=DG,连接BG,FG.
∵D是AB的中点,
∴AD=BD,
∵∠1=∠2,DE=DG,
∴△ADE≌△BDG,
∴AE=BG,∠A=∠3,
∵∠C =90°,
∴∠A+∠ABC=90°,
∴∠3+∠ABC=∠FBG=90°,
∴BG2+BF2=FG2,
∵AE=BG,
∴AE2+BF2=FG2,
∵DE=DG,∠EDF=90°,
∴FE=FG,
∴AE2+BF2=EF2,

(3)成立,如图,延长ED至G使得ED=DG,连接BG,FG,
∵D是AB的中点,
∴AD=BD,
∵∠1=∠2,DE=DG,
∴△ADE≌△BDG,
∴AE=BG,∠AED=∠BGD,
∵∠3=∠4,∠AED=∠BGD,
∴∠GBF=∠C=90°,
∵FD⊥ED,D为EG中点,
∴EF=FG,
在Rt△BFG中,BG2+BF2=FG2,
即AE2+BF2=EF2;


科目:初中数学 来源: 题型:
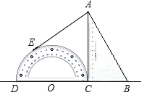
【题目】如图,将量角器和含![]() 角的一块直角三角板紧靠着放在同一平面内,使
角的一块直角三角板紧靠着放在同一平面内,使![]() ,
,![]() ,
,![]() 在一条直线上,且
在一条直线上,且![]() ,过点
,过点![]() 作量角器圆弧所在圆的切线,切点为
作量角器圆弧所在圆的切线,切点为![]() ,如果
,如果![]() ,则
,则![]() 的长是________
的长是________![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
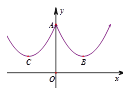
【题目】如图4所示的是桥梁的两条钢缆具有相同的抛物线形状.按照图中建立的直角坐标系,右面的一条抛物线的解析式为y=x2-4x+5表示,而且左右两条抛物线关于y轴对称,则左面钢缆的表达式为_________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=(2m-3)x+m+1经过点A(1,4)
(1)求m的值;
(2)画出此一次函数的图象;
(3)若一次函数交y轴于点B,求△OAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016广东省深圳市)荔枝是深圳的特色水果,小明的妈妈先购买了2千克桂味和3千克糯米糍,共花费90元;后又购买了1千克桂味和2千克糯米糍,共花费55元.(每次两种荔枝的售价都不变)
(1)求桂味和糯米糍的售价分别是每千克多少元;
(2)如果还需购买两种荔枝共12千克,要求糯米糍的数量不少于桂味数量的2倍,请设计一种购买方案,使所需总费用最低.
查看答案和解析>>
科目:初中数学 来源: 题型:
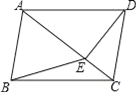
【题目】如图,在四边形ABCD中,AB∥CD,∠ABC=∠ADC,DE垂直于对角线AC,垂足是E,连接BE.
(1)求证:四边形ABCD是平行四边形;
(2)若AB=BE=2,sin∠ACD=![]() ,求四边形ABCD的面积.
,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据图①所示的程序,得到了如图②y与x的函数图像,若点M是y轴正半轴上任意一点,过点M作PQ∥x轴交图像于点P、Q,连接OP、OQ.则以下结论:
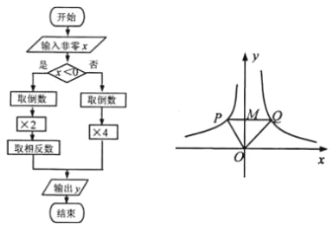
①x<0时,y=![]() ; ②△OPQ的面积为定值; ③x>0时,y随x的增大而增大;
; ②△OPQ的面积为定值; ③x>0时,y随x的增大而增大;
④MQ=2PM; ⑤∠POQ可以等于90°.
其中正确结论序号是
A. ①②③ B. ②③④ C. ③④⑤ D. ②④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017江苏省常州市)为了解某校学生的课余兴趣爱好情况,某调查小组设计了“阅读”、“打球”、“书法”和“其他”四个选项,用随机抽样的方法调查了该校部分学生的课余兴趣爱好情况(每个学生必须选一项且只能选一项),并根据调查结果绘制了如下统计图:
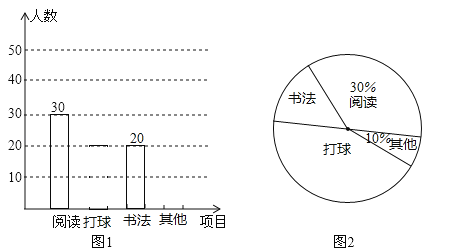
根据统计图所提供的信息,解答下列问题:
(1)本次抽样调查中的样本容量是 ;
(2)补全条形统计图;
(3)该校共有2000名学生,请根据统计结果估计该校课余兴趣爱好为“打球”的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com